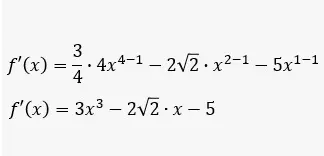Derivada de polinomios
Algunos de ellos son los que se indican a continuación,
Teorema 1: Si A y B son dos polinomios dados entonces,
deg(A ± B) ≤ max(deg A, deg B), con la igualdad si deg A ≠ deg B
deg(A⋅B) = deg A + deg B
Teorema 2: Dados los polinomios A y B ≠ 0, existen polinomios únicos Q (cociente) y R (residuo) tales que,
A = BQ + R y deg R < deg B
Teorema 3 (Teorema de Bezout): El polinomio P(x) es divisible por el binomio x – a, si y sólo si P(a) = 0.
Teorema 4: Si un polinomio P es divisible por un polinomio Q, entonces todo cero de Q es también un cero de P.
Teorema 5: El polinomio P(x) de grado n > 0 tiene una única representación de la forma P(x) = k(x – x1)(x – x2)…(x – xn), donde k ≠ 0 y x1,…,xn son números complejos, no necesariamente distintos.
Por tanto, P(x) tiene a lo sumo deg P = n ceros distintos.
Teorema 6: El polinomio de grado n-ésimo tiene exactamente n raíces complejas junto con sus multiplicidades.
Teorema 7: Si un polinomio P es divisible por dos polinomios coprimos Q y R, entonces es divisible por Q⋅R.
Teorema 8: Si ß es un cero de un polinomio real P(x), entonces también lo es
¯¯¯ ß .
Teorema 9: Un polinomio real P(x) tiene una factorización única (hasta el orden) de la forma
P(x) = (x – r1)…(x – rk)(x2 – p1x + q1)…(x2 – plx + ql),
donde ri y pj, qj son números reales con pi2 < 4qi y k + 2l = n.
Operaciones con polinomios
Las operaciones algebraicas básicas se pueden realizar sobre polinomios de diferentes tipos. Estas cuatro operaciones básicas sobre polinomios se pueden dar como,
- Suma de polinomios
- Sustracción de polinomios
- Multiplicación de polinomios
- División de polinomios
Suma de polinomios
La suma de polinomios es una de las operaciones básicas que utilizamos para aumentar o disminuir el valor de los polinomios. Tanto si quieres sumar números como si quieres sumar polinomios, las reglas básicas siguen siendo las mismas. La única diferencia es que cuando se trata de sumar 34 a 127, se alinean los valores de posición adecuados y se realiza la operación. Sin embargo, cuando se trata de sumar polinomios, hay que emparejar los términos iguales y luego sumarlos. De lo contrario, todas las reglas de la suma de números se trasladan a los polinomios. Echa un vistazo a la imagen que aparece aquí para entender cómo sumar dos polinomios cualesquiera.
Sustracción de polinomios
Como ya hemos comentado, las reglas para la resta de polinomios son muy similares a las de la resta de dos números. Sólo tenemos que alinear los polinomios dados en base a los términos semejantes.
Multiplicación de polinomios
La operación de multiplicación de polinomios sigue las propiedades generales como la propiedad conmutativa, la propiedad asociativa, la propiedad distributiva, etc. Aplicando estas propiedades utilizando las reglas de los exponentes podemos resolver la multiplicación de polinomios.
Por ejemplo, (2x + 3y)(4x – 5y) = 2x(4x – 5y) + 3y(4x – 5y) = 8×2 – 10xy + 12xy – 15y2
⇒ 8×2 + 2xy – 15y2
División de polinomios
La división de polinomios es una operación aritmética en la que dividimos un polinomio dado por otro polinomio que generalmente es de menor grado en comparación con el grado del dividendo.
Factorización de polinomios
La factorización de polinomios es el proceso por el cual descomponemos una expresión polinómica en la forma del producto de sus factores irreducibles, de forma que los coeficientes de los factores estén en el mismo dominio que el del polinomio principal. Existen diferentes técnicas que se pueden seguir para la factorización de polinomios, dadas como,
- Método de los factores comunes
- Método de agrupación
- Factorización por división de términos
- Factorización mediante identidades algebraicas
En función de la complejidad de la expresión polinómica dada, podemos seguir cualquiera de los métodos anteriores.
Ecuaciones polinómicas
Una ecuación polinómica es una ecuación formada con variables, exponentes y coeficientes junto con operaciones y un signo de igualdad. La forma general de una ecuación polinómica es P(x) = an xn + . . + rx + s. Algunos ejemplos de ecuaciones polinómicas son x2 + 3x + 2 = 0, x3 + x + 1 = 0, x + 7 = 0, etc.
Funciones polinómicas
Las expresiones generales que contienen variables de distintos grados, coeficientes, exponentes positivos y constantes se conocen como funciones polinómicas. He aquí algunos ejemplos de funciones polinómicas,
f(x) = x2 + 4
g(x) = -2×3 + x – 7
h(x) = 5×4 + x3 + 2×2
Resolución de polinomios
Resolver un polinomio significa encontrar las raíces o ceros de los polinomios. Podemos aplicar diferentes métodos para resolver un polinomio dependiendo del tipo de polinomio, ya sea un polinomio lineal, cuadrático, etc. Entendamos primero qué se entiende por el cero de un polinomio.
Ceros de los polinomios
Las raíces o ceros de un polinomio son los valores reales de la variable para los que el valor del polinomio se hace igual a cero. Así, si decimos que dos números reales cualesquiera, ‘α’ y ‘ß’ son ceros del polinomio p(x), si p(α) = 0 y p(ß) = 0. Por ejemplo, para un polinomio, p(x) = x2 – 2x + 1, observamos, p(1) = (1)2 – 2(1) + 1 = 0. Por tanto, 1 es un cero o raíz del polinomio dado. Esto también significa que (x – 1) es un factor de p(x).
Ahora, para encontrar el cero o raíz de cualquier polinomio, es decir, para resolver cualquier polinomio, podemos aplicar diferentes métodos,
- Factorización
- Método gráfico
- Método de Aciertos y Pruebas
Notas importantes sobre los polinomios
- Los términos de un polinomio sólo pueden estar separados por el signo ‘+’ o ‘-‘.
- Para que cualquier expresión se convierta en un polinomio, la potencia de la variable debe ser un número entero.
- La suma y la resta de un polinomio sólo son posibles entre términos semejantes.
- Todos los números del universo se llaman polinomios constantes.
Vídeos de Derivada de polinomios
Contenido