Cuartiles
Los cuartiles se encuentran cuando tenemos las series de datos ordenadas, es decir que para encontrar los cuartiles de la siguiente serie: {9,3,7,5,1,2,4,8}, habría que ordenarla primero, bien de menor a mayor: {1,2,3,4,5,7,8,9}, o bien de mayor a menor: {9,8,7,5,4,3,2,1}. La forma de ordenar las series dependerá del objetivo del estudio y de los análisis que busquemos, pero ambos tipos de orden son válidos para encontrar los cuartiles.
Los cuartiles se encuentran cuando se tiene una serie ordenada, es decir, que para encontrar los cuartiles en la siguiente serie: {9,3,7,5,1,2,4,8} esta tendría que ser ordenada primero, ya sea de menor a menor: {1,2,3,4,5,7,8,9} o de mayor a menor: {9,8,7,5,4,3,2,1}, el tipo de orden que se le dé a un conjunto de datos va a depender del propósito del estudio y del análisis que se le quiera dar a los datos recopilados, pero cualquiera de los órdenes que se le aplique a una serie de números es válido para encontrar los cuartiles.
Hay algunas veces en las que para analizar un problema desde diferentes perspectivas tenemos que encontrar los cuartiles dos veces, una de mayor a menor, y otra de menor a mayor, pero cuando encontramos los cuartiles de ambas maneras, sólo vamos a invertir el orden de los cuartiles, el primer cuartil será ahora el tercer cuartil, y el tercero será ahora el primer cuartil, porque la posición de estos 2 no van a cambiar, mientras que el segundo cuartil no cambiará en absoluto.
Posición de los cuartiles
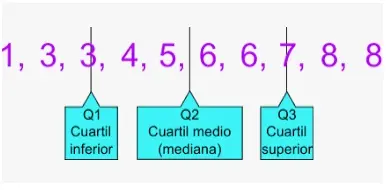
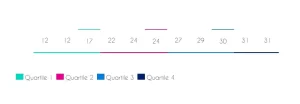
Los cuartiles son 3 números que dividen el conjunto de datos en 4 partes, donde hasta el primer cuartil hay un 25% de los datos, hasta el segundo cuartil hay un 50% de los datos y hasta el tercer cuartil hay un 75% de los datos.
El segundo cuartil siempre va a coincidir con la mediana, esto sucede porque el segundo cuartil, al igual que la mediana, es el número que está en el medio de una serie ordenada de números, y al igual que con la mediana, cuando el número total de datos es un número impar, entonces sólo vamos a tener un número central, pero cuando el número total de datos es par, entonces vamos a tener 2 números centrales, y en estos casos vamos a encontrar un promedio entre los números centrales, y el resultado será el segundo cuartil.
Otra propiedad de los cuartiles es que el primer cuartil estará en medio del primer número y el segundo cuartil, y el tercer cuartil estará en medio del segundo cuartil y el último número.
Cuartiles ejemplos
Para entender lo explicado anteriormente desarrollaremos el siguiente ejemplo: se midió la altura de los miembros de una empresa (en centímetros), encuentre los cuartiles de los resultados:
175
160
177
182
173
168
171
Lo primero que vamos a hacer es ordenar los números de menor a mayor.
160
168
171
173
175
177
182
Entonces vamos a encontrar el número central y este será el segundo cuartil.
160
168
171
173
175
177
182
Después tenemos que encontrar el número entre el segundo cuartil y el primer número y este será el primer cuartil.
160
168
171
173
175
177
182
Y por último tenemos que encontrar el número entre el segundo cuartil y el último número y será el tercer cuartil.
160
168
171
173
175
177
182
Los cuartiles permiten poder analizar los datos en porcentajes, en este caso el primer cuartil es 168, por lo que podemos decir que el 25% de los datos son iguales o inferiores a 168, el segundo cuartil es 173, por lo que el 50% de los datos son iguales o inferiores a 173, y por último, el tercer cuartil es 177, y como el cuarto cuartil es el 75%, el 75% de los datos son iguales o inferiores a 177.
Fórmula de los cuartiles
Hay casos en los que no podemos encontrar los cuartiles sólo viendo los datos, como hicimos en el último ejemplo, sino que cuando la cantidad de datos es mayor, encontrar los cuartiles es mucho más complejo, pero para estos casos existe una fórmula para encontrar la posición de cada cuartil.
Qk = k (n + 1)/4
En esta fórmula la letra Q es el cuartil y la variable «k» es el número de cuartil que queremos encontrar, «n» es el número total de datos (lo dividimos por 4 porque estamos encontrando cuartiles).
Vídeos de Cuartiles ejemplos
Contenido