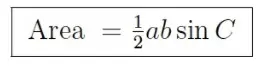Cuál es la base de un triángulo
Por ejemplo, existe la fórmula básica de que el área de un triángulo es la mitad de la base por la altura. Esta fórmula sólo funciona, por supuesto, cuando se conoce la altura del triángulo. Otra es la fórmula de Herón, que da el área en términos de los tres lados del triángulo, concretamente, como la raíz cuadrada del producto s(s – a)(s – b)(s – c), donde s es el semiperímetro del triángulo, es decir, s = (a + b + c)/2. Aquí consideraremos una fórmula para el área de un triángulo cuando se conocen dos lados y el ángulo incluido del triángulo. Supongamos que conocemos los valores de los dos lados a y b del triángulo, y el ángulo incluido C.
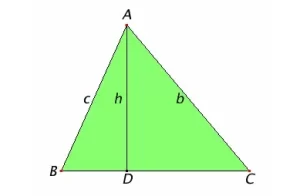
Al igual que en la demostración de la ley de los senos en el apartado anterior, deja caer una perpendicular AD desde el vértice A del triángulo hasta el lado BC, y etiqueta esta altura h. Entonces el triángulo ACD es un triángulo rectángulo, por lo que sin C es igual a h/b. Por lo tanto, h = b sin C. Como el área del triángulo es la mitad de la base a por la altura h, por lo tanto el área también es igual a la mitad de ab sin C. Aunque la figura es un triángulo agudo, puedes ver por la discusión en la sección anterior que h = b sin C se mantiene cuando el triángulo es recto u obtuso también. Por tanto, obtenemos la fórmula general
Un triángulo es un polígono que tiene tres lados y puede clasificarse en los siguientes tipos:
– Un triángulo equilátero tiene lados y ángulos iguales.
– El triángulo isósceles tiene dos lados iguales y dos ángulos iguales.
– Un triángulo escaleno tiene tres lados desiguales y tres ángulos desiguales.
– Un triángulo rectángulo tiene un ángulo recto (90°).
– Un triángulo acutángulo tiene todos los ángulos menores de 90°.
– Un triángulo obtusángulo tiene un ángulo mayor de 90°.
El perímetro de un triángulo = Suma de los tres lados
En la figura al lado del ΔABC, el perímetro es la suma de AB + BC + AC.
El área de un triángulo viene dada por:
A = ½ × Base × Altura
Cualquier lado del triángulo puede considerarse como su base.
Entonces, la longitud de la línea perpendicular desde el vértice opuesto se toma como la altura o altitud correspondiente.
Fórmulas adicionales para determinar el área de un triángulo:
Área de un triángulo = √(s(s-a)(s-b)(s-c)) por la Fórmula de Herón (o Fórmula de Hero), donde a, b y c son las longitudes de los lados del triángulo, y s = ½ (a + b + c) es el semiperímetro del triángulo.
Área de un triángulo equilátero
A= √(3) – ¼ – lado, donde lado = a = b = c
Área de un triángulo isósceles
A = ¼ -b – √(4a2 – b2)
Área del triángulo rectángulo
A= ½× Producto de los lados que contienen el ángulo recto.
Si se dan dos lados y el ángulo entre ellos, se puede determinar el área del triángulo mediante la siguiente fórmula:
Área = ½ – a – b – sinC = ½ – b – c – sinA = ½ – a – c – sin B
Hallar el área de un triángulo cuya base es 14 cm y la altura es 10 cm.
Solución:
b = 14 cm
h = 10 cm
A = ½ – 14 – 10 = 70 cm2
Halla el área de un triángulo cuyos lados y el ángulo entre ellos están dados como
a = 5cm y b = 7cm
C = 45o
Solución:
Área de un triángulo = ½ – a – b – sinC
Área = ½ × 5 ×7 × 0,707 (ya que sen 45 ° = 0,707)
Área = ½ × 24,745 = 12,3725 m2
Halla el área (en m2) de un triángulo isósceles, cuyos lados son 10 m y la base es12 m.
Solución:
El área de un triángulo isósceles viene determinada por:
A = ¼ -b – √(4a2 – b2)
A = ¼ -12 – √(4(10)2 – (12)2)
A = 48 m2
Vídeos de Cuál es la base de un triángulo
Contenido