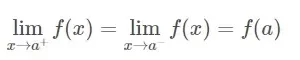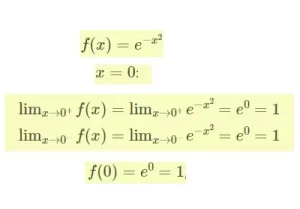Continuidad en un punto

por
Continuidad en un punto
Un polígono se llama polígono convexo cuando ningún segmento de línea entre los puntos, va dentro. Los límites del polígono convexo no van hacia el interior y todos los vértices apuntan hacia el exterior alejándose del centro. Hay muchos tipos de funciones y formas: funciones periódicas definidas a trozos, crecientes, decrecientes, huecas, convexas… Pero entre todas ellas, podemos clasificarlas bajo dos conjuntos más elementales: funciones continuas y no continuas.

Continuidad en un punto

La propiedad de la continuidad se manifiesta en varios aspectos de la naturaleza. El flujo de agua en los ríos es continuo. El flujo del tiempo en la vida humana es continuo, es decir, uno envejece continuamente. Y así sucesivamente. Del mismo modo, en matemáticas, tenemos la noción de continuidad de una función.

Lo que significa simplemente es que se dice que una función es continua si se puede trazar su curva en un gráfico sin levantar el bolígrafo ni una sola vez (siempre que se sepa dibujar bien). Es una definición muy sencilla y cercana a la realidad. Pero en aras de las matemáticas superiores, debemos definirla de forma más precisa.

Comúnmente se dice que una función es continua si es posible dibujarla sin necesidad de levantar el lápiz del papel y por tanto, dibujarla con un solo trazo.

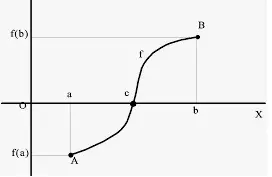
Matemáticamente la definición es un poco más elaborada. Consideremos una función f(x) . Diremos que es continua en el punto x=a si se cumple que los límites laterales de f(x) en x=a coinciden con el valor de la función en :

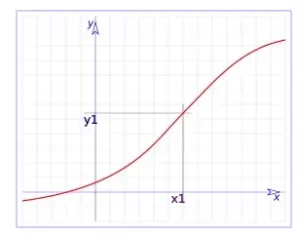
En el siguiente gráfico observamos una función continua.

y podemos ver que los límites laterales coinciden con el valor de la función con el punto x1, f(x1)=y1.

Definición de continuidad

Se dice que una función f(x) es continua en un punto x = a, en su dominio, si se cumplen las tres condiciones siguientes

  • f(a) existe (es decir, el valor de f(a) es finito)
  • Limx→a f(x) existe (es decir, el límite de la derecha = límite de la izquierda, y ambos son finitos)
  • Limx→a f(x) = f(a)

Se dice que la función f(x) es continua en el intervalo I = [x1,x2] si se cumplen las tres condiciones mencionadas anteriormente para cada punto del intervalo I.

Sin embargo, nótese que en los puntos extremos del intervalo I, no necesitamos considerar tanto los límites de la derecha como los de la izquierda para el cálculo de Limx→a f(x). Para a = x1, sólo hay que considerar el límite de la derecha, y para a = x2, sólo hay que considerar el límite de la izquierda.

Ejemplos de continuidad en un punto

 

 

Vídeos de Continuidad en un punto

Contenido