Conservacion de la energia mecanica
La energía mecánica es la suma de la energía cinética y la energía potencial de un objeto que se utiliza para realizar un trabajo determinado. En otras palabras, describe la energía de un objeto debido a su movimiento o posición, o ambos.
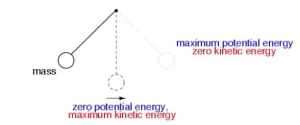
Consideremos el ejemplo de un péndulo simple ideal (sin fricción). Podemos ver que la energía mecánica de este sistema es una combinación de su energía cinética y su energía potencial gravitatoria. A medida que el péndulo oscila hacia adelante y hacia atrás, se produce un intercambio constante entre la energía cinética y la energía potencial. Cuando la bobina alcanza su máxima altura, la energía potencial del sistema es la más alta, mientras que la energía cinética es cero.
En la posición media, la energía cinética es la más alta y la energía potencial es cero. Entre estos dos puntos extremos, vemos que el sistema posee tanto energía cinética como potencial, cuya suma es constante. Estas observaciones nos dicen mucho sobre la conservación de la energía mecánica. Pero, ¿cómo podemos demostrarlo para cualquier otro sistema? En la siguiente sección, aprenderemos más sobre la conservación de la energía mecánica utilizando un ejemplo adecuado.
Según el principio de conservación de la energía mecánica
La energía mecánica total de un sistema se conserva, es decir, la energía no puede crearse ni destruirse; sólo puede convertirse internamente de una forma a otra si las fuerzas que realizan trabajo sobre el sistema son de naturaleza conservativa.
Para comprender mejor esta afirmación, consideremos un ejemplo de movimiento unidimensional de un sistema. Aquí un cuerpo, bajo la acción de una fuerza conservativa F, se desplaza en Δx, entonces a partir del teorema trabajo-energía, podemos decir que la red realizada por todas las fuerzas que actúan sobre un sistema es igual al cambio en la energía cinética del sistema.
Matemáticamente, ΔKE = F(x) Δx
Donde, ΔK es el cambio en la energía cinética del sistema. Considerando que sólo actúan fuerzas conservativas sobre el sistema Wnet = Wc.
Por lo tanto Wc = ΔKE
Además, si las fuerzas conservativas hacen el trabajo en un sistema, el sistema pierde energía potencial igual al trabajo realizado. Por lo tanto, Wc = -PE.
Lo que implica que la energía cinética total y la energía potencial de un sistema permanecen constantes si el proceso involucra sólo fuerzas conservativas.
KE + PE = constante
KEi+ PEi = KEf+ PEf
Donde denota los valores iniciales y f los valores finales de KE y PE.
Esta ley se aplica sólo en la medida en que las fuerzas son de naturaleza conservativa. La energía mecánica del sistema se define como la energía cinética total más la energía potencial total. En un sistema que comprende sólo fuerzas conservativas, cada fuerza está asociada a una forma de energía potencial y la energía sólo cambia entre la energía cinética y los diferentes tipos de energía potencial, de manera que, la energía total permanece constante.
Vídeos de Conservacion de la energia mecanica
Contenido