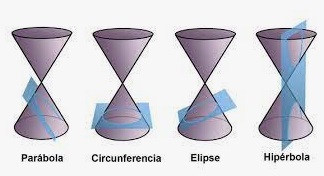
Conicas
Un cono es un objeto geométrico sólido tridimensional que tiene una base circular y un borde puntiagudo en la parte superior llamado vértice. Tiene una superficie curva y una base circular, un vértice y una arista.
Los elementos de un cono son el radio, la altura y la altura oblicua. El radio es la distancia entre el centro de la base circular y un punto cualquiera de la circunferencia de la base. La altura del cono es la distancia entre el vértice del cono y el centro de la base circular. La altura de la inclinación es la distancia entre el vértice del cono y cualquier punto de la circunferencia del cono.
¿Cómo encontrar el volumen de un cono?
En un cono, la longitud perpendicular entre el vértice de un cono y el centro de la base circular se conoce como la altura (h) de un cono. Las líneas inclinadas de un cono son la longitud (L) de un cono a lo largo de la superficie curva cónica. Todos estos parámetros se mencionan en la figura anterior.
Para hallar el volumen de un cono, se necesitan los siguientes parámetros
El radio (r) de la base circular,
La altura o la inclinación de un cono.
Como todos los demás volúmenes, el volumen de un cono también se expresa en unidades cúbicas.
Fórmula del volumen de un cono
El volumen de un cono es igual a un tercio del producto del área de la base por la altura. La fórmula del volumen se representa como
Volumen de un cono = ⅓ x πr2 x h
V = ⅓ πr2 h
Donde V es el volumen, r es el radio y h, la altura.
La altura oblicua, el radio y la altura de un cono se relacionan como;
Altura oblicua de un cono, L = √(r2+h2) ………. (Teorema de Pitágoras)
Vídeos de Conicas
Contenido