Composición de funciones
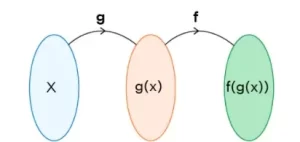
La composición de funciones f(x) y g(x) en la que g(x) actúa primero se representa por f(g(x)) o (f ∘ g)(x). Combina dos o más funciones para dar lugar a otra función. En la composición de funciones, la salida de una función que está dentro del paréntesis se convierte en la entrada de la función exterior. es decir,
En f(g(x)), g(x) es la entrada de f(x).
En g(f(x)), f(x) es la entrada de g(x).
Podemos entenderlo con la siguiente figura:
es decir, para encontrar f(g(x)) (que se lee como «f de g de x»), tenemos que encontrar primero g(x) y luego sustituimos el resultado en f(x).
Símbolo de la composición de funciones
El símbolo de la composición de funciones es ∘. También se puede mostrar sin usar este símbolo pero usando los paréntesis. es decir
(f ∘ g)(x) = f(g(x)) y se lee como «f de g de x». Aquí, g es la función interna y f es la función externa.
(g ∘ f)(x) = g(f(x)) y se lee como «g de f de x». Aquí, f es la función interna y g es la función externa.
¿Cómo se resuelven las funciones compuestas?
Usando BODMAS, siempre simplificamos primero lo que está entre paréntesis. Así que para encontrar f(g(x)), primero hay que calcular g(x) y sustituirla dentro de f(x). Del mismo modo, para encontrar g(f(x)), primero hay que calcular f(x) y sustituirla en g(x). Es decir, al encontrar las funciones compuestas, el orden importa. Esto significa que f(g(x)) puede NO ser igual a g(f(x)). Para dos funciones cualesquiera f(x) y g(x), encontramos la función compuesta f(g(a)) mediante los siguientes pasos:
Hallar g(a) sustituyendo x = a en g(x).
Hallar f(g(a)) sustituyendo x = g(a) en f(x).
Podemos entender estos pasos con el siguiente ejemplo. Aquí estamos encontrando f(g(-1)) cuando f(x) = x2 – 2x y g(x) = x – 5.
Podemos resumir este proceso mediante un simple cálculo matemático como el que se muestra a continuación:
f(g(-1)) = f(-1-5)
= f(-6)
= (-6)2 – 2 (-6)
= 36 + 12
= 48
Hallar la función compuesta a partir de la gráfica
Para encontrar la función compuesta de dos funciones (que no están definidas algebraicamente) mostradas gráficamente, debemos recordar que si (x, y) es un punto en una función f(x) entonces f(x) = y. Usando esto, para encontrar f(g(a)) (es decir, f(g(x)) en x = a):
Encuentra primero g(a) (es decir, la coordenada y en la gráfica de g(x) que corresponde a x = a)
Encuentra f(g(a)) (es decir, la coordenada y en la gráfica de f(x) que corresponde a g(a))
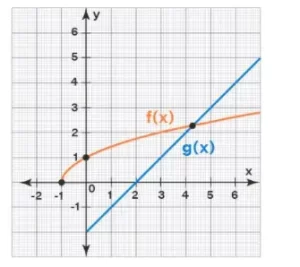
Ejemplo: Hallar f(g(5)) a partir de la siguiente gráfica.
Solución:
f(g(5)) = f(3) (Porque g(5) = 3 ya que (5, 3) está en g(x))
= 2 (Porque f(3) = 2 ya que (3, 2) está en f(x))
Por lo tanto, f(g(5)) = 2.
Dominio de las funciones compuestas
En general, si g : X → Y y f : Y → Z entonces f ∘ g : X → Z. es decir, el dominio de f ∘ g es X y su rango es Z. Pero cuando las funciones están definidas algebraicamente, aquí están los pasos para encontrar el dominio de la función compuesta f(g(x)).
- Hallar el dominio de la función interna g(x) (Sea A)
- Hallar el dominio de la función obtenida al hallar f(g(x)) (Sea B)
- Halla la intersección de A y B y A ∩ B da el dominio de f(g(x))
Ejemplo: Hallar el dominio de f(g(x)) cuando f(x) = 1/(x+2) y g(x) = 1/(x+3).
Solución:
En f(g(x)), la función interior es g(x) y su dominio es A = {x | x ≠ -3}.
Ahora vamos a calcular f(g(x)).
Su dominio es B = {x : x ≠ -7/2}
Así, el dominio de f(g(x)) es, A ∩ B = {x : x ≠ -3 y x ≠ -7/2}.
Esto en la notación de intervalo es (-∞, -7/2) U (-7/2, -3) U (-3, ∞).
Vídeos de Composición de funciones
Contenido