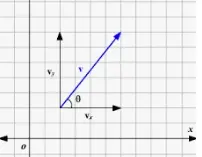
Componente de un vector
Supongamos que un vector V está definido en un plano bidimensional. El vector V se divide en dos componentes como vx y vy
Ahora dejemos que un ángulo θ, se forme entre el vector V y la componente x del vector. El vector V y su componente x (vx) forman un triángulo rectángulo si trazamos una línea paralela a la componente y (vy).
Por las razones trigonométricas, sabemos
- cos θ = Lado adyacente/Hipotenusa = vx/V
- sin θ = Lado opuesto/Hipotenusa = vy/V
donde V es la magnitud del vector V.
Fórmula de las componentes del vector
Como en el apartado anterior hemos derivado la expresión
cos θ = vx/V
sin θ = vy/V
Por tanto, la fórmula para hallar las componentes de un vector cualquiera pasa a ser
vx=V cos θ
vy=Vsin θ
Donde V es la magnitud del vector V y se puede encontrar utilizando el teorema de Pitágoras;
|V| = √(vx2, vy2)
Vectores ortogonales
Los vectores se pueden representar fácilmente utilizando el sistema de coordenadas en tres dimensiones. Antes de entrar en la representación de los vectores, entendamos qué es la representación ortogonal.
En términos de geometría de coordenadas, por representación ortogonal entendemos los parámetros que se encuentran en ángulo recto entre sí. En un sistema tridimensional ortogonal, tenemos tres ejes perpendiculares entre sí, que representan los ejes x, y y z.
¿Qué son los componentes de un vector?
La división de un vector en sus 2 componentes respectivas dirigidas a lo largo de los ejes respectivos se llama componentes del vector. Este proceso se llama «resolución de un vector o vector en un plano».
Supongamos que existe un vector AB en un sistema de coordenadas bidimensional con los ejes x e y. Si este vector no está perfectamente alineado con los ejes de coordenadas, entonces el vector AB debe formar algún ángulo con los ejes de coordenadas.
Para encontrar la dirección y la magnitud de dicho vector que forma un ángulo en un plano bidimensional, el vector AB se divide en 2 componentes correspondientes. Las dos componentes resultantes se alinean con los ejes x e y.
Las dos componentes en las que se resuelve el vector (digamos AB) están dirigidas en las direcciones horizontal y vertical. Tras la división del vector AB en sus componentes, se puede concluir que el vector AB es la resultante de sus 2 componentes, cada una dirigida a lo largo de un eje.
Esta teoría se puede demostrar aplicando la regla de la cabeza a la cola. Consideremos un vector AB en un espacio bidimensional. Podemos analizar que las dos componentes son AC y BC como se muestra en la figura siguiente:
Aplicando la regla de cabeza a cola, podemos observar que la cola de AC coincide con la cola del vector AB, y la cabeza del componente vectorial BC coincide con la cabeza del vector AB, concluyendo así el vector AB como la resultante de sus dos componentes vectoriales.
Matemáticamente, se puede expresar como
AB = AC + BC
O
|AB| = |AC| + |BC|
Vídeos de Componente de un vector
Contenido