Área del octógono
Área de un octógono = 2a2(1+√2)
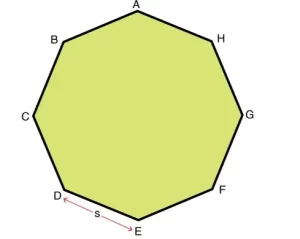
Donde «a» es la longitud de un lado cualquiera del octógono.
Propiedades de un octógono regular
Antes de seguir adelante y deducir la fórmula del área de un octógono, vamos a repasar algunas de las propiedades básicas de un octógono regular.
- Tiene 8 lados y 8 ángulos interiores.
- Todos los lados tienen la misma longitud y todos los ángulos tienen la misma medida.
- Hay un total de 20 diagonales en un octógono regular.
- Cada ángulo interior mide 135 grados. Por tanto, la suma de todos los ángulos interiores es (135 x 8) = 1080 grados.
- Cada ángulo exterior mide 45 grados. Por lo tanto, la suma de todos los ángulos exteriores es (45 x 8) = 360 grados.
Área de un octógono regular
La fórmula más utilizada para calcular el área de un octógono regular viene dada por A = 2a2 (1 + √2), donde a representa la longitud de cada lado del octágono dado. Para derivar esta ecuación, considera el pentágono dado. Dibujando todas sus diagonales lo hemos dividido en 8 triángulos isósceles con el centro como vértice común.
La fórmula del área de un octógono es 2 veces (1 + la raíz cuadrada de 2) por la longitud del lado al cuadrado. Aquí, a es la longitud de un lado.
8in
1 + la raíz cuadrada de 2 = 2,414.
8 al cuadrado = 64.
2 x 2,414 x 64 = 308,992 pulgadas cuadradas
Como 308,992 pulgadas cuadradas es demasiado grande para el espacio que Kevin tiene para hacer su edificio, los lados de 8 pulgadas no funcionarán. Ahora vamos a probar la fórmula utilizando 5 pulgadas para cada lado.
Ejemplo de área del octógono
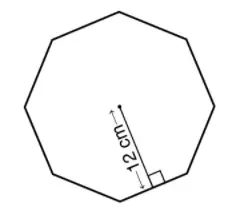
Halla el área de un octógono regular cuyo perímetro es de 128 cm y su apotema es de 12 cm.
Solución:
Como sabemos
Área (A) = 1/2 × P × a, aquí P = 128 cm, a = 12 cm
= 1/2 × P × a,
= 1/2 × 128 × 12
= 768 cm cuadrados
Vídeos de Área del octógono
Contenido