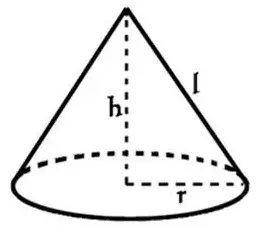
Area de un cono
El primer paso para hallar la superficie de un cono es medir el radio de la parte circular del cono. El siguiente paso es hallar el área del círculo, o base. El área de un círculo es 3,14 veces el radio al cuadrado (πr2). Ahora, tendrás que encontrar el área del cono en sí. Para ello, debes medir el lado (altura de la inclinación) del cono. Asegúrate de utilizar la misma forma de medición que el radio.
Ahora puedes utilizar la medida del lado para hallar el área del cono. La fórmula del área de un cono es 3,14 veces el radio por el lado (πrl).
Así que el área del cono es igual al área del círculo más el área del cono y la fórmula final viene dada por
SA = πr2 + πrl
Donde,
r es el radio
h es la altura
l es la altura oblicua
El área de la superficie curva (lateral) de un cono = πrl
Un cono tiene un radio de 3 cm y una altura de 5 cm, halla la superficie total del cono.
Solución:
- Para empezar tenemos que encontrar la altura de la inclinación del cono, que se determina utilizando Pitágoras, ya que la sección transversal es un triángulo rectángulo.
l2 = h2 + r2
l2 = 52 + 32
l2 = 25 + 9
l = √(34)
l = 5,83 cm
Y la superficie total del cono es:
SA = πr2 + πrl
SA = π – r – (r + l)
SA = π – 3 – (3 + 5,83)
SA = 83,17 cm2
Por lo tanto, la superficie total del cono es de 83,17 cm2
- La superficie total de un cono es de 375 pulgadas cuadradas. Si su altura oblicua es cuatro veces el radio, ¿cuál es el diámetro de la base del cono? Usa π = 3.
Solución:
La superficie total de un cono = πrl + πr2 = 375 pulgadas2
Altura oblicua: l = 4 × radio = 4r
Sustituye l = 4r y π = 3
3 × r × 4 r + 3 × r2 = 375
12r2 + 3r2 = 375
15r2 = 375
r2 = 25
r = 25
r = 5
Así que el radio de la base del cono es de 5 pulgadas.
Y el diámetro de la base del cono = 2 × radio = 2 × 5 = 10 pulgadas.
- Cuál es la superficie total de un cono si su radio = 4 cm y su altura = 3 cm.
Solución:
Como se mencionó anteriormente la fórmula para el área de la superficie de un cono está dada por:
SA = πr2 + πrl
SA = πr(r + l)
Como en el ejemplo anterior, la inclinación se puede determinar mediante Pitágoras:
l2 = h2 + r2
l2 = 32 + 42
l2 = 9 + 16
l = 5
Insertando l = 5 obtendremos
SA = πr(r + l)
SA = 3,14 – 4 – (4+5)
SA = 113,04 cm2
- La altura oblicua de un cono es de 20 cm. el diámetro de la base es de 15 cm. Halla el área de la superficie curva del cono.
Solución:
Dado que,
Altura oblicua: l = 20cm
Diámetro: d = 15cm
Radio: r = d/2 = 15/2 = 7,5cm
Superficie curva = πrl
CSA = πrl
CSA =π – 7,5 – 20
CSA =471,24 cm2
Vídeos de Area de un cono
Contenido