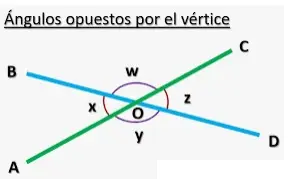
Angulos opuestos
Los ángulos verticales son un par de ángulos no adyacentes formados por la intersección de dos rectas. En palabras sencillas, los ángulos verticales se sitúan uno frente al otro en las esquinas de la «X» formada por dos rectas. También se denominan ángulos verticalmente opuestos, ya que están situados uno frente al otro.
Teorema de los ángulos verticales
El teorema de los ángulos verticales o teorema de los ángulos verticalmente opuestos afirma que dos ángulos verticales opuestos que se forman cuando dos rectas se cruzan son siempre iguales (congruentes) entre sí.
Afirmación: Los ángulos verticales (los ángulos opuestos que se forman cuando dos líneas se cruzan) son congruentes.
La prueba es sencilla y se basa en los ángulos rectos. Ya sabemos que los ángulos de una recta suman 180°.
Teorema de los ángulos verticales
∠1 + ∠2 = 180° (Ya que son un par de ángulos lineales) ——— (1)
∠1 +∠4 = 180° (Ya que son un par de ángulos lineales) ——— (2)
De las ecuaciones (1) y (2), ∠1 + ∠2 = 180° = ∠1 +∠4.
Según la propiedad transitiva, si a = b y b = c entonces a = c.
Por tanto, podemos reescribir el enunciado como ∠1 + ∠2 = ∠1 +∠4. ——–(3)
Eliminando ∠1 en ambos lados de la ecuación (3), obtenemos ∠2 = ∠4.
Del mismo modo, podemos utilizar el mismo conjunto de afirmaciones para demostrar que ∠1 = ∠3. Por tanto, concluimos que los ángulos verticalmente opuestos son siempre iguales.
Para encontrar la medida de los ángulos en la figura, utilizamos la propiedad del ángulo recto y el teorema del ángulo vertical simultáneamente.
Los ángulos verticales son ángulos pares que se forman cuando dos líneas se cruzan. Los ángulos verticales se denominan a veces ángulos verticalmente opuestos porque los ángulos son opuestos entre sí.
Los escenarios de la vida real en los que se utilizan los ángulos verticales son: la señal de cruce de ferrocarril, la letra «X», las tijeras abiertas, etc. Los egipcios solían dibujar dos líneas que se cruzaban y siempre medían los ángulos verticales para confirmar que ambos eran iguales.
Los ángulos verticales son siempre iguales entre sí. En general, podemos decir que, se forman 2 pares de ángulos verticales cuando dos líneas se cruzan. Observa el siguiente diagrama.
En el diagrama anterior:
∠a y ∠b son ángulos verticales opuestos. Los dos ángulos también son iguales, es decir, ∠a = ∠
∠c y ∠d forman otro par de ángulos verticales y también son iguales.
También podemos decir que los dos ángulos verticales comparten un vértice común (el punto final común de dos o más rectas o rayos).
Prueba del teorema del ángulo vertical
Podemos demostrar en el diagrama anterior que.
Sabemos que el ángulo b y el ángulo d son ángulos suplementarios, es decir
También sabemos que el ángulo a y el ángulo d son ángulos suplementarios, es decir
Podemos reordenar las ecuaciones anteriores:
Comparando las dos ecuaciones, tenemos:
Por lo tanto, demostrado.
Los ángulos verticales son ángulos suplementarios cuando las líneas se cruzan perpendicularmente.
Por ejemplo, ∠W y ∠ Y son ángulos verticales que también son ángulos suplementarios. Del mismo modo, ∠X y ∠Z son ángulos verticales suplementarios.
Vídeos de Angulos opuestos
Contenido