Intervalo de confianza
Un intervalo de confianza muestra la probabilidad de que un parámetro se sitúe entre un par de valores en torno a la media.
Los intervalos de confianza miden el grado de incertidumbre o certeza de un método de muestreo.
La mayoría de las veces se construyen utilizando niveles de confianza del 95% o del 99%.
Entender los intervalos de confianza
Los intervalos de confianza miden el grado de incertidumbre o certeza de un método de muestreo. Pueden adoptar cualquier número de límites de probabilidad, siendo el más común un nivel de confianza del 95% o del 99%. Los intervalos de confianza se realizan mediante métodos estadísticos, como la prueba t.
Los estadísticos utilizan los intervalos de confianza para medir la incertidumbre en una variable de la muestra. Por ejemplo, un investigador selecciona diferentes muestras al azar de la misma población y calcula un intervalo de confianza para cada muestra para ver cómo puede representar el verdadero valor de la variable poblacional. Los conjuntos de datos resultantes son todos diferentes; algunos intervalos incluyen el verdadero parámetro poblacional y otros no.
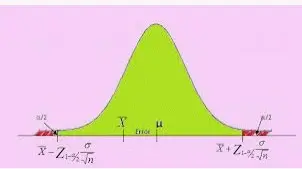
Un intervalo de confianza es un rango de valores, delimitado por encima y por debajo de la media de la estadística, que probablemente contenga un parámetro poblacional desconocido. El nivel de confianza se refiere al porcentaje de probabilidad, o certeza, de que el intervalo de confianza contenga el verdadero parámetro poblacional cuando se extrae una muestra aleatoria muchas veces. O, en la lengua vernácula, «estamos seguros al 99% (nivel de confianza) de que la mayoría de estas muestras (intervalos de confianza) contienen el verdadero parámetro poblacional».
El mayor error en relación con los intervalos de confianza es que representan el porcentaje de datos de una muestra determinada que se encuentra entre los límites superior e inferior. Por ejemplo, uno podría interpretar erróneamente el mencionado intervalo de confianza del 99% de 70 a 78 pulgadas como si indicara que el 99% de los datos de una muestra aleatoria se encuentra entre estos números. Esto es incorrecto, aunque existe un método de análisis estadístico independiente para hacer tal determinación. Para ello hay que identificar la media y la desviación estándar de la muestra y trazar estas cifras en una curva de campana.
Cálculo del intervalo de confianza
Supongamos que un grupo de investigadores estudia la altura de los jugadores de baloncesto de un instituto. Los investigadores toman una muestra aleatoria de la población y establecen una altura media de 74 pulgadas.
La media de 74 pulgadas es una estimación puntual de la media de la población. Una estimación puntual por sí misma tiene una utilidad limitada porque no revela la incertidumbre asociada a la estimación; no se tiene una buena idea de lo lejos que puede estar esta media muestral de 74 pulgadas de la media poblacional. Lo que falta es el grado de incertidumbre de esta única muestra.
Los intervalos de confianza proporcionan más información que las estimaciones puntuales. Al establecer un intervalo de confianza del 95% utilizando la media y la desviación estándar de la muestra, y asumiendo una distribución normal representada por la curva de campana, los investigadores llegan a un límite superior e inferior que contiene la verdadera media el 95% de las veces.
Supongamos que el intervalo está entre 72 y 76 pulgadas. Si los investigadores toman 100 muestras aleatorias de la población de jugadores de baloncesto de la escuela secundaria en su conjunto, la media debería estar entre 72 y 76 pulgadas en 95 de esas muestras.
Si los investigadores quieren una confianza aún mayor, pueden ampliar el intervalo al 99% de confianza. Hacerlo crea invariablemente un intervalo más amplio, ya que da cabida a un mayor número de medias muestrales. Si establecen que el intervalo de confianza del 99% está entre 70 y 78 pulgadas, pueden esperar que 99 de las 100 muestras evaluadas contengan un valor medio entre estas cifras.
Un nivel de confianza del 90%, por otro lado, implica que esperaríamos que el 90% de las estimaciones del intervalo incluyeran el parámetro poblacional, y así sucesivamente.
Vídeos de Intervalo de confianza
Contenido