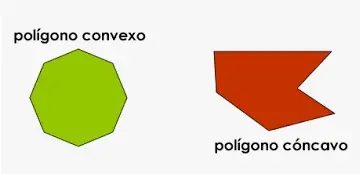
Polígono cóncavo
Un polígono simple es considerado como polígono cóncavo si y sólo si al menos uno de los ángulos interiores es un ángulo reflejo (entre 180° y 360°). También se denomina polígono no convexo. El área y el perímetro del mismo dependerán de la forma del polígono concreto.
Un polígono tiene al menos un ángulo que mide más de 180 grados, lo que se denomina polígono cóncavo. Los vértices (puntos extremos) de este polígono están hacia dentro y hacia fuera. Son justo lo contrario de los polígonos convexos. Un triángulo no puede considerarse un polígono cóncavo porque sólo tiene tres lados y la suma de sus ángulos interiores es de 180 grados.
Polígono cóncavo irregular
Un polígono puede ser convexo o cóncavo. Estos polígonos se clasifican a su vez en regulares o irregulares. El polígono irregular puede tener lados con diferentes medidas y también cada una de las medidas de los ángulos interiores son también variadas. Se observa que todos los polígonos cóncavos son irregulares ya que los ángulos interiores del polígono son de diferentes medidas.
Sí, una estrella es un polígono cóncavo. Porque un polígono cóncavo debe tener al menos 4 lados. Además, uno o más ángulos interiores deben ser mayores de 180 grados.
Polígono cóncavo regular
Un polígono regular es un polígono donde la longitud de cada lado es la misma y todos los ángulos interiores son iguales. Según la definición de polígono cóncavo, contiene al menos uno de los ángulos interiores mayor que 180 grados. Además, la suma de los ángulos interiores de un polígono es (n – 2) x 180, donde n es el número de lados. Por lo tanto, no es posible tener un polígono con todos los lados iguales y un ángulo mayor de 180 grados. Por lo tanto, los polígonos regulares nunca son cóncavos.
Área de un polígono cóncavo
A diferencia de un polígono regular, no hay una fórmula fácil para encontrar el área de un polígono cóncavo. Cada lado puede tener una longitud diferente y cada ángulo interior puede ser diferente. Así que tenemos que dividir el polígono cóncavo en triángulos o paralelogramos u otras formas para las que podamos encontrar fácilmente el área.
Área de un polígono cóncavo = Área de las diferentes formas disponibles en él
Perímetro de un polígono cóncavo
El perímetro de cualquier polígono se define como la distancia total recorrida alrededor del límite del polígono. Del mismo modo, el perímetro de un polígono cóncavo se define como la distancia total recorrida alrededor del límite del polígono cóncavo. El perímetro de un polígono cóncavo se puede encontrar sumando la longitud de todos los lados.
El perímetro de un polígono cóncavo = Suma de todos sus lados
Propiedades de los polígonos cóncavos
Las siguientes son algunas de las propiedades importantes de un polígono cóncavo:
- Un polígono cóncavo tiene al menos un vértice que apunta hacia adentro para dar la forma cóncava
- Tiene al menos un ángulo reflejo. Significa que al menos uno de los ángulos interiores es mayor que 180° y menor que 360°
- Si se traza un segmento de línea que atraviese el polígono cóncavo, éste intersectará el límite más de dos veces
- Un polígono puede tener más de una diagonal que quede fuera del límite
- Un polígono cóncavo tiene al menos un par de lados que unen un vértice que va fuera del vértice
- Podemos dividir un polígono cóncavo en un conjunto de polígonos convexos
- Un triángulo no puede ser un polígono cóncavo
Ángulo exterior de un polígono cóncavo
Los ángulos exteriores de un polígono siempre suman 3600. Un polígono cóncavo tiene uno o más de sus vértices «empujados hacia dentro». Por lo tanto, apuntan hacia el interior del polígono
Ángulo interior de un polígono cóncavo
Los ángulos interiores de cualquier polígono siempre suman un valor constante, que sólo depende del número de lados del polígono. Por ejemplo, los ángulos interiores de un pentágono siempre suman 5400, sin importar si es convexo o cóncavo, o qué tamaño y forma tenga. La fórmula de la suma de los ángulos interiores de un polígono viene dada por
Suma de ángulos interiores = 180 * (n – 2) grados
donde n es el número de lados.
- Cuadrado: n = 4; suma de ángulos interiores = 180 x (4-2) = 360 grados
- Pentágono: n = 5; suma de los ángulos interiores = 180 x (5-2) = 540 grados
- Hexágono: n = 6; suma de los ángulos interiores = 180 x (6-2) = 720 grados
Vídeos de Polígono cóncavo
Contenido