Excentricidad de la hiperbola
Los dos términos importantes a los que debemos referirnos antes de hablar de la excentricidad son el foco y la directriz de la hipérbola. Para una sección cónica, el lugar de cualquier punto de la misma es tal que la relación entre su distancia al punto fijo -foco- y su distancia a la recta fija -directriz- es un valor constante, que se denomina excentricidad.
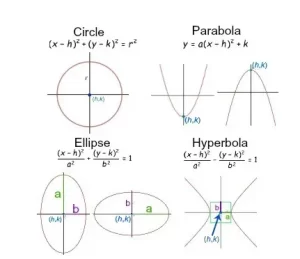
Una característica que poseen todas las secciones cónicas es la excentricidad. La excentricidad de una sección cónica nos indica lo cerca que está de tener la forma de un círculo. Cuanto más se aleja la excentricidad de una sección cónica de 0, menos se parece la forma a un círculo.
Vuelve a mirar las formas cónicas. Un círculo es un círculo, así que obviamente la excentricidad de un círculo es 0. ¿Cuál de las otras tres secciones cónicas crees que se acercaría más a la forma de un círculo?
Bueno, una elipse se parece a un círculo comprimido. Cuando se compara con las otras dos formas cónicas, es la que más se parece a un círculo. Un razonamiento similar permite deducir que la parábola sería la siguiente más cercana, y la hipérbola la más alejada de la forma de un círculo.
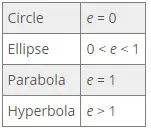
El gráfico siguiente proporciona rangos de valores de la excentricidad (e) para cada una de las secciones cónicas.
Las dos secciones cónicas con las excentricidades más fáciles de recordar son el círculo (e = 0) y la parábola (e = 1). La elipse y la hipérbola son un poco más complicadas, pero no mucho. Podemos encontrar el valor exacto de la excentricidad de estas dos formas cónicas utilizando sus ecuaciones.
La excentricidad de una elipse (x – h)2 / a2 + (y – k)2 / b2 = 1 estará siempre entre 0 y 1 y puede calcularse mediante las siguientes fórmulas:
Cuando a > b, utilizamos e = √(a2 – b2) / a.
Cuando b > a, utilizamos e = √(b2 – a2) / b.
La excentricidad de una hipérbola (x – h)2 / a2 – (y – k)2 / b2 = 1 es siempre mayor que 1 y se puede calcular mediante la siguiente fórmula:
e = √(a2 + b2) / a.
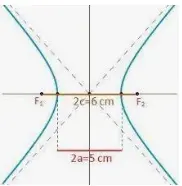
Cuando hay un conjunto de puntos en un plano determinado, y la diferencia de la distancia de dos puntos fijos permanece constante, se llama una hipérbola. También podemos decir que la distancia del foco en el plano tiene la relación constante, que es mayor que la directriz (línea fija) en el plano.
En la hipérbola, encontramos que la longitud del eje transversal es 2a y la longitud del eje conjugado es 2b. Además, según la regla de excentricidad, «la distancia entre los dos focos de una hipérbola es 2c». La relación de excentricidad de una hipérbola es c: a, donde c es la distancia desde el centro de la hipérbola a cualquier foco. Y a es el semieje mayor.
La c (distancia del centro de la hipérbola a cualquier foco) es mayor que igual a a (semieje mayor), es decir, c ≥ a. La excentricidad de la hipérbola es siempre mayor que 1, es decir, e > 1. La fórmula de la excentricidad de una hipérbola puede escribirse como a2 + b2, donde b es la longitud del semieje menor; así, la distancia entre dos focos se convierte en 2ae.
Vídeos de Excentricidad de la hiperbola
https://www.youtube.com/watch?v=4Zqj3uhn6ts
Contenido