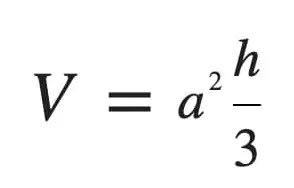Apotema de una pirámide
La fórmula del volumen de una pirámide cuadrada V es
donde a es la longitud del lado de la base y h es la distancia perpendicular de la base al vértice, también conocida como la altura perpendicular de la pirámide.
Ten en cuenta que a2 es también el área de un cuadrado de lado a. Por tanto, parte del cálculo requerirá encontrar el área de la base, que se mide en unidades cuadradas. Por lo tanto, la fórmula también se puede escribir como
V = ⅓ Bh
donde la base
b = a2
De hecho, la fórmula generalizada es
Volumen de una pirámide cuadrada V = 1/3 x base x altura
Esta fórmula puede utilizarse para hallar el volumen de cualquier pirámide de base poligonal siempre que se pueda calcular el área de la base, siempre que la altura h sea la distancia perpendicular del vértice al plano que contiene la base.
La altura h puede calcularse de varias maneras, eligiendo fórmulas trigonométricas específicas en función de los valores conocidos.
El volumen V calculado mediante la fórmula se medirá en unidades cúbicas.
La unidad está determinada por la medida de cada variable involucrada en el cálculo, es decir, a y h. Ambas variables necesitan ser medidas en, o convertidas a, las mismas unidades antes de ser usadas en la fórmula.
Ejemplo de cómo calcular el volumen de una pirámide cuadrada
Se pueden hacer muchas preguntas diferentes sobre el volumen de una pirámide cuadrada. Normalmente, las preguntas del examen te pedirán que encuentres una variable desconocida necesaria para la fórmula del volumen utilizando algunos valores conocidos. A continuación se presentan algunos ejemplos utilizando la misma pirámide de base cuadrada para una mejor comprensión.
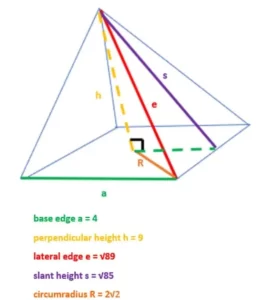
Ejemplo 1: Encontrar el Volumen cuando se conoce la altura de una pirámide y la longitud de la base.
Este es el problema más sencillo con el que te vas a encontrar ya que todas las variables necesarias están dadas. Sustituye los valores de a y h directamente en la fórmula.
V = ⅓ x 42 x 9 = 48 m3
donde m3 es la unidad de medida y representa los metros cúbicos. Esto se debe a que el área de la base cuadrada es de 4m x 4m = 16 m3 o 16 metros cuadrados. Este valor se multiplica por la altura, que es de 9 metros. Por tanto, tenemos un producto de valores de tres metros: m x m x m = m3.
Vídeos de Apotema de una pirámide
Contenido