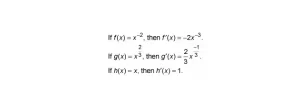Derivada de la funcion inversa
La diferenciación es un método para calcular la tasa a la que cambia una variable dependiente y con respecto al cambio en la variable independiente x. Esta tasa de cambio se llama la derivada de y con respecto a x. Hay muchas notaciones diferentes para denotar «tomar la derivada de». La relación entre y y x se suele denotar por f(x) y su derivada se suele denotar como f'(x) o y’ o dy/dx. La definición de la derivada viene dada por:
que es un procedimiento largo utilizado para evaluar la derivada de una función. Afortunadamente, se han desarrollado métodos más sencillos para ayudar a evaluar las derivadas más rápidamente.
El siguiente diagrama muestra las reglas básicas de la derivada que pueden ser útiles: Regla Constante, Regla Múltiple Constante, Regla de la Potencia, Regla de la Suma, Regla de la Diferencia, Regla del Producto, Regla del Cociente y Regla de la Cadena.
Algunas reglas de diferenciación son fáciles de recordar y utilizar. Entre ellas están la regla de la constante, la regla de la potencia, la regla del múltiplo constante, la regla de la suma y la regla de la diferencia.
La regla de la constante: Es sencilla. f (x) = 5 es una recta horizontal con pendiente cero, por lo que su derivada también es cero.
La regla de la potencia:
Para repetirla, se adelanta la potencia y se reduce la potencia en 1. Eso es todo.
La regla de la potencia funciona para cualquier potencia: una positiva, una negativa o una fracción.
Asegúrate de que recuerdas cómo hacer la última función. Es la función más sencilla, pero el problema más fácil de pasar por alto. Por cierto, ¿ves cómo encontrar esta última derivada sigue la regla de la potencia? (Pista: x a la potencia cero es igual a uno).
Puedes diferenciar funciones radicales reescribiéndolas como funciones de potencia y utilizando la regla de la potencia.
La regla del múltiplo constante: ¿Qué pasa si la función que estás diferenciando comienza con un coeficiente? No hay ninguna diferencia. Un coeficiente no tiene ningún efecto en el proceso de diferenciación. Simplemente lo ignoras y diferencias según la regla apropiada. El coeficiente se queda donde está hasta el último paso, cuando simplificas tu respuesta multiplicando por el coeficiente.
No olvides que ð (~3.14) y e (~2.72) son números, no variables, por lo que se comportan como números ordinarios. Las constantes de los problemas, como c y k, también se comportan como números ordinarios. Así, por ejemplo
La regla de la suma: Cuando quieras la derivada de una suma de términos, toma la derivada de cada término por separado.
La regla de la diferencia: Si tienes una diferencia (es decir, una resta) en lugar de una suma, no hay ninguna diferencia. Sigues diferenciando cada término por separado.
Los signos de suma y resta no se ven afectados por la diferenciación.
Vídeos de Derivada de la funcion inversa
Contenido