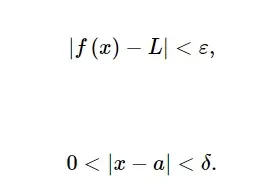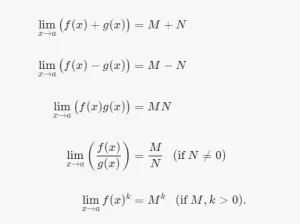Limites exponenciales

En matemáticas, un límite se define como el valor al que se aproxima una función para los valores de entrada dados. Los límites son importantes en el cálculo y el análisis matemático y se utilizan para definir las integrales, las derivadas y la continuidad. Se utiliza en el proceso de análisis y siempre se refiere al comportamiento de la función en un punto determinado. El límite de una sucesión se generaliza en el concepto de límite de una red topológica y se relaciona con el límite y el límite directo en la categoría de teoría. En general, las integrales se clasifican en dos tipos: integrales definidas e indefinidas. En las integrales definidas, el límite superior y el límite inferior están definidos correctamente. Mientras que en las indefinidas las integrales se expresan sin límites, y tendrá una constante arbitraria al integrar la función.

Limites exponenciales

Sea f (x) una función que está definida en un intervalo abierto X que contiene a x = a. (No es necesario que el valor f (a) esté definido).

El número L se llama límite de la función f (x) a medida que x → a si y sólo si, para cada ε > 0 existe δ > 0 tal que:

Esta definición se conoce como ε-δ- o definición de Cauchy para el límite.

También existe la definición de Heine del límite de una función f(x), que establece que una función tiene un límite L en x=a , si para cada secuencia xn , que tiene un límite en a la secuencia f(xn) tiene un límite L.Las definiciones de Heine y Cauchy del límite de una función son equivalentes.

El límite de una función en un punto aa de su dominio (si existe) es el valor al que se aproxima la función a medida que su argumento se acerca a a.a. El concepto de límite es el concepto fundamental del cálculo y del análisis. Se utiliza para definir la derivada y la integral definida, y también puede utilizarse para analizar el comportamiento local de las funciones cerca de los puntos de interés.

Informalmente, se dice que una función tiene un límite L en a si es posible hacer que la función se acerque arbitrariamente a L eligiendo valores cada vez más cercanos a a. Nótese que el valor real en a es irrelevante para el valor del límite.

Propiedades de los límites

Las propiedades más importantes de los límites son las propiedades algebraicas, que dicen esencialmente que los límites respetan las operaciones algebraicas:

Vídeos de Limites exponenciales

Contenido