Como sacar el apotema de un pentagono
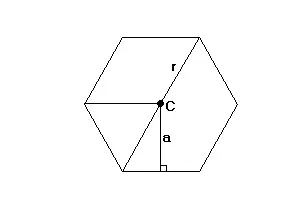
La apotema de un polígono regular es la mediatriz de cualquier lado en el que tenga su punto final. Un ángulo central de un polígono regular es un ángulo cuyo vértice es el centro y cuyos rayos, o lados, contienen los puntos extremos de un lado del polígono regular. Así, un polígono regular de n lados tiene n apotemas y n ángulos centrales, cada uno de los cuales mide 360/n grados. Cada apotema es la bisectriz del ángulo central que contiene el lado al que se extiende el apotema. A continuación se muestran estas características de un polígono regular.
Una vez dominadas estas nuevas definiciones, la fórmula del área de un polígono regular es fácil. El área de un polígono regular es la mitad del producto de su apotema por su perímetro. A menudo la fórmula se escribe así Área=1/2(ap), donde a denota la longitud de un apotema, y p denota el perímetro.
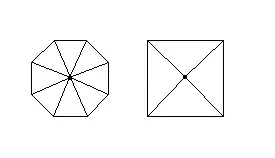
Cuando un polígono de n lados se divide en n triángulos, su área es igual a la suma de las áreas de los triángulos. ¿Puedes ver cómo 1/2(ap) es igual a la suma de las áreas de los triángulos que forman un polígono regular? La apotema es igual a la altura, y el perímetro es igual a la suma de las bases. Así que 1/2(ap) es sólo una forma un poco más sencilla de expresar la suma de las áreas de los n triángulos que forman un polígono regular de n lados.
Vídeos de Como sacar el apotema de un pentagono
Contenido