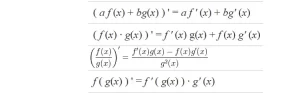Reglas de la derivada
Las reglas importantes de la diferenciación son
- Regla de la potencia
- Regla de la suma y la diferencia
- Regla del producto
- Regla del cociente
- Regla de la cadena
Regla de la Potencia de la Diferenciación
Esta es una de las reglas más comunes de las derivadas. Si x es una variable y se eleva a una potencia n, entonces la derivada de x elevada a la potencia se representa por
d/dx(xn) = nxn-1
- Ejemplo: Hallar la derivada de x5
Solución: Según la regla de la potencia, sabemos que
d/dx(xn) = nxn-1
Por tanto, d/dx(x5) = 5×5-1 = 5×4
Regla de la suma de la diferenciación
Si la función es suma o diferencia de dos funciones, entonces la derivada de las funciones es la suma o diferencia de las funciones individuales, es decir
Si f(x)=u(x)±v(x), entonces
f'(x)=u'(x)±v'(x)
- Ejemplo 1: f(x) = x + x3
Solución: Aplicando aquí la regla de la suma de la derivada, tenemos:
f'(x) = u'(x) + v'(x)
Ahora, diferenciando la función dada, obtenemos;
f'(x) = d/dx(x + x3)
f'(x) = d/dx(x) + d/dx(x3)
f'(x) = 1 + 3×2
- Ejemplo 2: Hallar la derivada de la función f(x) = 6×2 – 4x.
Solución:
La función dada es: f(x) = 6×2 – 4x
Es de la forma f(x) = u(x) – v(x)
Así que aplicando la regla de las diferencias de las derivadas, obtenemos
f'(x) = d/dx (6×2) – d/dx(4x)
= 6(2x) – 4(1)
= 12x – 4
Por tanto, f'(x) = 12x – 4
Regla del producto de las derivadas
Según la regla del producto de las derivadas, si la función f(x) es el producto de dos funciones u(x) y v(x), entonces la derivada de la función viene dada por:
Si f(x) = u(x)×v(x), entonces:
f′(x) = u′(x) × v(x) + u(x) × v′(x)
Ejemplo: Hallar la derivada de x2(x+3).
Solución: Según la regla del producto de la derivada, sabemos;
f′(x) = u′(x) × v(x) + u(x) × v′(x)
Aquí,
u(x) = x2 y v(x) = x+3
Por tanto, al diferenciar la función dada, obtenemos
f'(x) = d/dx[x2(x+3)]
f'(x) = d/dx(x2)(x+3)+x2d/dx(x+3)
f'(x) = 2x(x+3)+x2(1)
f'(x) = 2×2+6x+x2
f'(x) = 3×2+6x
f'(x) = 3x(x+2)
Reglas de derivación
Vídeos de Reglas de la derivada
Contenido