Baricentro
En Geometría, el centroide es un concepto importante relacionado con un triángulo. Un triángulo es una figura acotada de tres lados con tres ángulos interiores. En función de los lados y los ángulos, un triángulo puede clasificarse en diferentes tipos como
- Triángulo escaleno
- Triángulo isósceles
- Triángulo equilátero
- Triángulo acutado
- Triángulo obtuso
- Triángulo rectángulo
El centroide es una propiedad importante de un triángulo. Vamos a discutir la definición de centroide, la fórmula, las propiedades y el centroide para diferentes formas geométricas en detalle.
Definición de Baricentro
El centroide es el punto central del objeto. El punto en el que se cruzan las tres medianas del triángulo se conoce como centroide de un triángulo. También se define como el punto de intersección de las tres medianas. La mediana es una línea que une el punto medio de un lado y el vértice opuesto del triángulo. El centroide del triángulo separa la mediana en la proporción de 2: 1. Se puede hallar sacando la media de los puntos de las coordenadas x e y de todos los vértices del triángulo.
Teorema del Baricentro
El teorema del centroide afirma que el centroide del triángulo está a 2/3 de la distancia del vértice al punto medio de los lados.
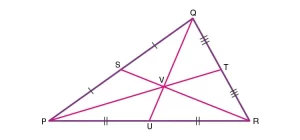
Supongamos que PQR es un triángulo cuyo centroide es V. S, T y U son los puntos medios de los lados del triángulo PQ, QR y PR, respectivamente. Por tanto, según el teorema
QV = 2/3 QU, PV = 2/3 PT y RV = 2/3 RS
Baricentro de un triángulo rectángulo
El centroide de un triángulo rectángulo es el punto de intersección de tres medianas, trazadas desde los vértices del triángulo hasta el punto medio de los lados opuestos.
Baricentro de un cuadrado
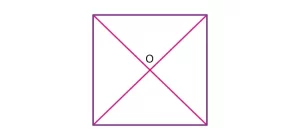
El punto de intersección de las diagonales del cuadrado es el centroide del cuadrado. Como todos sabemos, el cuadrado tiene todos sus lados iguales. Por lo tanto, es fácil localizar el centroide en él. Mira la siguiente figura, donde O es el centroide del cuadrado.
Propiedades del Baricentro
Las propiedades del centroide son las siguientes:
- El centroide es el centro del objeto.
- Es el centro de gravedad.
- Siempre debe estar dentro del objeto.
- Es el punto de concurrencia de las medianas.
Fórmula del Baricentro
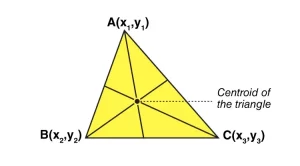
Consideremos un triángulo. Si los tres vértices del triángulo son A(x1, y1), B(x2, y2), C(x3, y3), el centroide de un triángulo puede calcularse tomando la media de los puntos de las coordenadas X e Y de los tres vértices. Por lo tanto, el centroide de un triángulo se puede escribir como
Centroide de un triángulo = ((x1+x2+x3)/3, (y1+y2+y3)/3)
Vídeos de Baricentro
Contenido