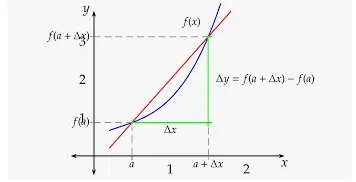
Diferencial de una funcion
La diferenciación significa la tasa de cambio de una cantidad con respecto a otra. La velocidad se calcula como la tasa de cambio de la distancia con respecto al tiempo. Esta velocidad en cada instante no es la misma que la media calculada. La velocidad es lo mismo que la pendiente, que no es otra cosa que la tasa de cambio instantánea de la distancia en un período de tiempo.
La relación de un pequeño cambio en una cantidad con un pequeño cambio en otra que depende de la primera cantidad se llama diferenciación. Uno de los conceptos importantes del cálculo se centra principalmente en la diferenciación de una función. El valor máximo o mínimo de una función, la velocidad y la aceleración de los objetos en movimiento y la tangente de una curva se determinan mediante la diferenciación. Si y = f(x) es diferenciable, entonces la diferenciación se representa como f'(x) o dy/dx.
Definición de las derivadas
El significado geométrico de la derivada de y = f(x) es la pendiente de la tangente a la curva y = f(x) en ( x, f(x)). El primer principio de la diferenciación es calcular la derivada de la función utilizando los límites. Sea una función de una curva y = f(x). Tomemos un punto P con coordenadas(x, f(x)) en una curva. Tomemos otro punto Q con coordenadas (x+h, f(x+h)) sobre la curva. Ahora PQ es la secante de la curva. La pendiente de una curva en un punto es la pendiente de la recta tangente en ese punto. Sabemos que la pendiente de la recta secante es y2-y1/x2-x1.
Diferenciación de funciones elementales
La derivada de una función constante es 0. si y = k, donde k es una constante, entonces y’ = 0
La derivada de una función potencia: Si y = xn , n > 0. Entonces y’ = n x n-1
La derivada de funciones logarítmicas: Si y = ln e x, entonces y’ = 1/x y si y = log a x, entonces y’ = 1/[(log a) x]
La derivada de una función exponencial: Si y = a x , y = ax log a
Diferenciación de funciones trigonométricas
Si y = sen x, y’ = cos x
Si y = cos x, y’ = -sin x
Si y = tan x, y’ = sec2 x
Si y = sec x, y’ = sec x tan x
Si y = cosec x, y’ = -cosec x cot x
Si y = cot x, y’ = -cosec2 x
Reglas de diferenciación
Si f es diferenciable en un punto x = x 0 entonces f es continua en x 0 . Una función es diferenciable en un intervalo [a,b] si es diferenciable en cada punto [a,b]. La suma, la diferencia, el producto y el compuesto de funciones diferenciables, dondequiera que estén definidas, son diferenciables, y el cociente de dos funciones diferenciables es diferenciable, dondequiera que esté definido. Las reglas de diferenciación son las siguientes:
- Regla de la suma: Si y = u(x) ± v(x), entonces dy/dx = du/dx ± dv/dx.
- Regla del producto: Si y = u(x) × v(x), entonces dy/dx = u.dv/dx + v.du/dx
- Regla del cociente: Si y = u(x) ÷ v(x), entonces dy/dx = (v.du/dx- u.dv/dx)/ v2
- Regla de la cadena: Sea y = f(u) una función de u y si u=g(x) de modo que y = f(g(x), entonces d/dx(f(g(x))= f'(g(x))g'(x)
- Regla constante: y = k f(x), k ≠ 0, entonces d/dx(k(f(x)) = k d/dx f(x).
Vídeos de Diferencial de una funcion
Contenido