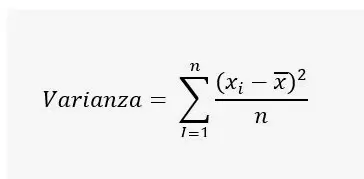Formula varianza
La varianza es una medida de la diferencia entre los puntos de datos y la media. Según Layman, la varianza es una medida de la distancia que separa un conjunto de datos (números) de su valor medio (promedio).
La varianza significa encontrar la diferencia esperada de la desviación del valor real. Por lo tanto, la varianza depende de la desviación estándar del conjunto de datos dado.
Cuanto mayor sea el valor de la varianza, los datos estarán más dispersos de su media y si el valor de la varianza es bajo o mínimo, entonces estarán menos dispersos de la media. Por lo tanto, se denomina medida de dispersión de los datos con respecto a la media.
La varianza de la muestra se utiliza para calcular la variabilidad de una muestra determinada. Una muestra es un conjunto de observaciones que se extraen de una población y pueden representarla completamente. La varianza de la muestra se mide con respecto a la media del conjunto de datos. También se conoce como varianza estimada.
Como los datos pueden ser de dos tipos, agrupados y no agrupados, hay dos fórmulas disponibles para calcular la varianza de la muestra. Además, la raíz cuadrada de la varianza muestral da como resultado la desviación estándar de la muestra.
¿Qué es la varianza de la muestra?
La varianza de la muestra se utiliza para medir la dispersión de los puntos de datos de un determinado conjunto de datos en torno a la media. Todas las observaciones de un grupo se conocen como la población. Cuando el número de observaciones empieza a aumentar, resulta difícil calcular la varianza de la población. En esta situación, se elige un número determinado de observaciones que pueden utilizarse para describir todo el grupo. Este conjunto específico de observaciones forma una muestra y la varianza así calculada es la varianza de la muestra.
Definición de la varianza de la muestra
La varianza de la muestra puede definirse como la expectativa de la diferencia al cuadrado de los puntos de datos con respecto a la media del conjunto de datos. Es una medida absoluta de dispersión y se utiliza para comprobar la desviación de los puntos de datos con respecto a la media de los mismos.
Ejemplo de varianza muestral
Supongamos que un conjunto de datos está dado como 3, 21, 98, 17 y 9. Se determina la media (29,6) del conjunto de datos. Se resta la media de cada punto de datos y se toma la suma del cuadrado de los valores resultantes. Esto da 6043,2. Para obtener la varianza de la muestra, este número se divide por uno menos que el número total de observaciones. Así, la varianza de la muestra es de 1510,8.
Vídeos de Formula varianza
Contenido