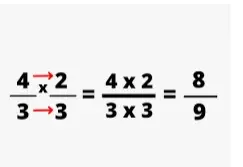Multiplicación de fracciones con igual denominador

Multiplicación de fracciones: Cuando una fracción se multiplica por otra fracción la resultante es una fracción o un número entero. Sabemos que una fracción tiene dos partes: numerador y denominador. Por tanto, cuando multiplicamos dos fracciones cualesquiera, se multiplican los numeradores y los denominadores, respectivamente. Un ejemplo de multiplicación de fracciones es ⅔ x ¼ = (2 x 1)/(3 x 4) = 2/12 = ⅙. La multiplicación de fracciones no es como la suma o la resta de fracciones, donde los denominadores de ambas fracciones deben ser iguales. Dos fracciones pueden multiplicarse fácilmente, aunque los denominadores sean diferentes. Al multiplicar fracciones, hay que tener en cuenta que las fracciones pueden ser una fracción propia o impropia, pero no pueden ser una fracción mixta.

Multiplicación de fracciones

Digamos que tienes 1/2 de una galleta y ahora tu madre quiere que compartas tu 1/2 a partes iguales con tu hermano. Por lo tanto, tienes que darle 1/2 de tu 1/2 a tu hermano. ¿Qué parte de la galleta vais a recibir tú y tu hermano? Para averiguarlo, tendrás que multiplicar fracciones.

Antes de llegar a eso, hagamos un rápido repaso. Como recordarás, las fracciones son partes de un todo. Están formadas por un numerador, o el número de arriba, y un denominador, o el número de abajo.

Cuando aprendiste a sumar y restar fracciones, aprendiste que primero debes tener denominadores iguales, es decir, que los denominadores son el mismo número, y los denominadores se mantienen iguales cuando sumas o restas las fracciones. Sin embargo, cuando multiplicamos fracciones con denominadores iguales, esa ya no es la regla. En su lugar, ¡obtendremos un denominador totalmente diferente!

Multiplicación de fracciones con igual denominador

¡Multiplicar fracciones es tan fácil como 1 – 2 – 3!

Paso 1: Multiplica los numeradores.

Paso 2: Multiplicar los denominadores.

Paso 3: Simplificar el resultado final.

Simplificar significa convertir la fracción en los números más pequeños posibles, encontrando el mayor número que pueda dividir tanto el numerador como el denominador. Por ejemplo, 2/4 puede simplificarse a 1/2 porque tanto el numerador como el denominador pueden dividirse por 2. Así que 2/4 ÷ 2/2 = 1/2. Usamos 1/2 porque es más fácil de ver y entender. Pongamos a prueba nuestros tres pasos.

Multipliquemos 3/4 * 1/4 siguiendo nuestros tres sencillos pasos:

Paso 1: Multiplicar los numeradores.

3/4 * 1/4 = 3 * 1 = 3

Paso 2: Multiplicar los denominadores.

3/4 * 1/4 = 4 * 4 = 16

Así que nuestra respuesta a 3/4 * 1/4 = 3/16. No olvides el paso 3.

Paso 3: Simplificar.

¿Hay algún número, además del 1, que pueda entrar tanto en el 3 como en el 16? No, resulta que no lo hay. Por lo tanto, ¡3/16 es lo más simplificado que se puede hacer!

Multipliquemos 3/10 * 5/10. No olvides tus pasos.

Paso 1: Multiplica los numeradores.

3/10 * 5/10 = 3 * 5 = 15

Paso 2: Multiplica los denominadores.

3/10 * 5/10 = 10 * 10 = 100

Paso 3: Simplificar.

15/100 es nuestro resultado final, así que ¿qué números se nos ocurren que nos ayuden a simplificar? El único número que puede encajar será el número 5. Así que queremos dividir 15 entre 5 para que sea igual a 3 y 100 entre 5 para que sea igual a 20. 15/100 se simplifica a 3/20. Simplificar las fracciones puede hacer que sean más fáciles de trabajar.

Vídeos de Multiplicación de fracciones con igual denominador

Contenido