Perímetro del paralelogramo
El perímetro de un paralelogramo es la longitud de la línea continua que forma su límite. Su unidad es la misma que la de sus lados. Un cuadrilátero es una forma cerrada formada por cuatro segmentos de recta. Un cuadrilátero se llama paralelogramo si sus lados opuestos son paralelos y tienen la misma longitud. Algunos ejemplos de paralelogramo son el rombo, el rectángulo y el cuadrado. Estas son algunas de las propiedades de un paralelogramo.
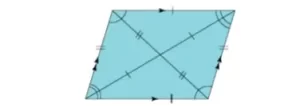
- Los lados opuestos son iguales.
- Los ángulos opuestos son iguales.
- Las diagonales se bisecan entre sí.
- Cada dos ángulos adyacentes son complementarios.
¿Qué es el perímetro del paralelogramo?
El perímetro de un paralelogramo es la longitud de su contorno y, por tanto, es igual a la suma de todos sus lados. Pero es posible que siempre no conozcamos todos los lados de un paralelogramo. En cambio, puede que nos den otra información sobre el paralelogramo y nos pidan que encontremos su perímetro. El perímetro de un paralelogramo se puede encontrar en los siguientes casos.
- Cuando se conocen dos lados adyacentes.
- Cuando se conoce un lado y las diagonales.
- Cuando se conocen la base, la altura y un ángulo cualquiera.
Fórmula del perímetro del paralelogramo con los lados
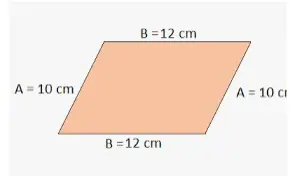
Como ya hemos comentado, el perímetro de un paralelogramo es la suma de las longitudes de todos sus lados. Sabemos que los lados opuestos de un paralelogramo son iguales. Consideremos un paralelogramo con dos lados adyacentes que son ‘a’ y ‘b’ (entonces los otros dos lados adyacentes también serán ‘a’ y ‘b’ solamente).
Fórmula del perímetro del paralelogramo con lados
Entonces el perímetro del paralelogramo es a + b + a + b (o) 2a + 2b (o) 2 (a + b). Por lo tanto, el perímetro (P) de un paralelogramo con lados es,
P = 2 (a + b) unidades.
Ejemplo: Hallar el perímetro de un paralelogramo cuyos lados adyacentes son 5 unidades y 9 unidades.
Solución:
Los lados adyacentes del paralelogramo dado son, a = 5 unidades y b = 9 unidades. Entonces su perímetro (P) es,
P = 2 (a + b)
P = 2 (5 + 9) = 2 (14) = 28 unidades.
Fórmula del perímetro del paralelogramo con un lado y diagonales
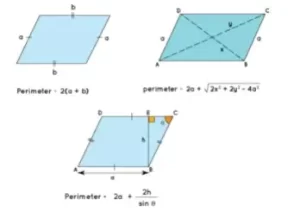
Consideremos un paralelogramo con lados ‘a’ y ‘b’ y diagonales ‘x’ e ‘y’. Supongamos que los valores del lado ‘a’, y las diagonales ‘x’ e ‘y’ están dados pero el valor de ‘b’ no está dado y se nos pide que encontremos el perímetro del paralelogramo.
Fórmula del perímetro del paralelogramo con un lado y diagonales
Aplicando la ley de los cosenos para el triángulo ABD,
x2 = a2 + b2 – 2ab cos ∠BAD
Aplicando la regla del coseno para el triángulo ADC,
y2 = a2 + b2 – 2ab cos ∠ADC
Sumando las dos ecuaciones anteriores,
x2 + y2 = 2a2 + 2b2 – 2ab (cos ∠BAD + cos ∠ADC) …. (1)
Sabemos que dos ángulos adyacentes cualesquiera de un paralelogramo (es una propiedad de los paralelogramos) son suplementarios. Así que
∠BAD + ∠ADC = 180o
∠BAD = 180o – ∠ADC
Aplicando cos en ambos lados,
cos ∠BAD = cos (180o – ∠ADC) = – cos ∠ADC
Sustituyendo esto en (1),
x2 + y2 = 2a2 + 2b2 – 2ab ( – cos ∠ADC + cos ∠ADC)
x2 + y2 = 2a2 + 2b2 – 2ab (0)
x2 + y2 = 2a2 + 2b2
Hemos obtenido la relación entre los lados y las diagonales del paralelogramo. Ahora vamos a resolverla para ‘b’, ya que no se nos ha dado la longitud de ‘b’.
2b2 = x2 + y2 – 2a2
b2 = (x2 + y2 – 2a2) / 2
b = √ [(x2 + y2 – 2a2) / 2]
Ahora conocemos los lados del paralelogramo (‘a’ y ‘b’) y por tanto podemos utilizar la fórmula del apartado anterior para hallar su perímetro (P).
P = 2a + 2b
P = 2a + 2 √ [(x2 + y2 – 2a2) / 2]
P = 2a + √[2(x2 + y2 – 2a2)
P = 2a + √(2×2 + 2y2 – 4a2)
Vídeos de Perímetro del paralelogramo
Contenido