Cono
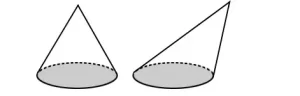
Un cono, normalmente denominado cono circular, es una figura geométrica en 3D que tiene una base circular y llega a un punto fuera de la base. A continuación se muestran dos tipos de conos.
Es posible que cada vez que oiga la palabra cono piense en un cono de tráfico o en un cono de helado.
Clasificación de los conos
El segmento de línea que va del vértice al centro de la base circular del cono, a menudo denominado eje del cono, se utiliza para clasificarlo como cono recto o cono oblicuo. El eje de un cono recto es perpendicular a su base circular. El eje de un cono recto es también la altura del cono. El eje de un cono oblicuo no es perpendicular a su base.
Secciones transversales de los conos
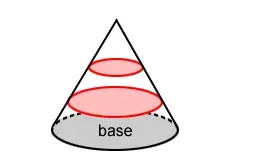
Un plano de corte es un plano que corta a un cono, formando una sección transversal. Dependiendo de la forma en que el plano de corte corte al cono, se forma una forma diferente. Cualquier sección transversal paralela a la base de un cono circular forma un círculo que es similar (todos los círculos son similares) a la base. Esto es cierto para cualquier sección transversal paralela de un cono.
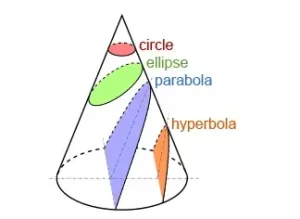
Si el plano de corte no es paralelo a la base de un cono circular, la sección transversal tiene la forma de una elipse, una parábola o una hipérbola, como se muestra en la figura siguiente. Una parábola se forma cuando el plano de corte es paralelo a la línea de altura oblicua opuesta.

Superficie de un cono circular recto
La superficie total de un cono circular recto es
A = πr2 + πrs
donde r es el radio de la base y s es la altura oblicua. En la ecuación, πr2 es el área de la base y πrs es el área de la superficie lateral.
Si cortamos a lo largo de la altura oblicua de un cono circular recto y lo colocamos en posición horizontal, obtenemos una superficie lateral plana, o sector circular, como se muestra arriba. El arco de este sector es la circunferencia de la base, que es 2πr.
Propiedades de un cono
- Una cara circular
- Un vértice
- Una base circular y una curva continua
- El vértice es un punto sobre el centro de la base
- Los embudos tienen forma de cono
- Los helados se venden en cucuruchos
- Los sombreros de cumpleaños tienen forma de cono
Ejemplo de cono
- Hallar la superficie total del cono circular recto que aparece a continuación.
Podemos usar el Teorema de Pitágoras para encontrar la altura de la inclinación, s.
s2 = 62 + 82 = 100
s = 10
Utilizando la fórmula de la superficie total con r = 6 y s = 10
A = π×62 + π×6×10
A = 96π o 301,59
- Halla la superficie total de un cono de radio 14 unidades y altura oblicua 8 unidades. (Usa π = 22/7)
Solución: Las dimensiones dadas son, radio del cono (r) = 14 unidades y altura oblicua (l) = 8 unidades.
Sustituyendo los valores en la fórmula de la superficie total del cono
πr (r + l) = (22/7) × 14 × (14 + 8)
⇒ 22 × 2 × 22
⇒ 968 unidades cuadradas
Respuesta: La superficie total del cono es de 968 unidades cuadradas.
Vídeos de Cono
Contenido