Convexo y cóncavo

Ya conoces la derivada de una función. Representa la tasa de cambio instantánea de una función en un periodo determinado. El proceso de calcular las derivadas de la función se conoce como diferenciación. Cuando una función se diferencia una vez, la derivada resultante se conoce como primera derivada. Podemos seguir diferenciando la primera derivada para calcular la segunda derivada de la función y repetir el proceso hasta que la función deje de ser diferenciable. Todas las derivadas posteriores a la primera derivada se conocen como derivadas de orden superior. Aunque la primera derivada proporciona información crítica sobre la función, no la describe completamente.

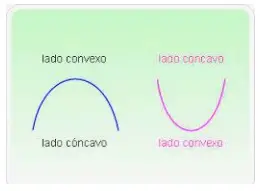
Convexo y cóncavo

La segunda derivada de la función representa cómo se curva la función, a diferencia de la primera derivada que nos habla de la pendiente de la función tangente. Una función que tiene una primera derivada creciente se curva hacia arriba y se conoce como función convexa. Por otro lado, una función que tiene una primera derivada decreciente se conoce como función cóncava y se curva hacia abajo. También describimos una función cóncava como el negativo de una función convexa. En lugar de decir que una función es cóncava, también podemos decir que es cóncava hacia abajo porque una función cóncava siempre se curva hacia abajo.

En el siguiente apartado veremos cómo identificar la curva de la función y describirla como función cóncava o convexa a través de sus segundas derivadas.

Teorema

Si la función f y su derivada f’ se pueden diferenciar en a, entonces:

La f es convexa en a si f »(a) >0
La f es cóncava en a si f »(a) < 0

Ahora, procedamos a resolver algunos ejemplos para determinar que la función es cóncava o convexa.

Ejemplos

Identifica la curva de la siguiente función y determina si es una función cóncava o convexa:

f (x) = 3x^2 + 7x – 9

Solución

En primer lugar, calcularemos la primera derivada de la función empleando las reglas de suma/diferencia y potencia de la diferenciación:

f ‘ (x) = 6x + 7

Ahora diferenciaremos la primera derivada para calcular la segunda derivada de la función:

f » (x) = 6

Ahora, compara los resultados con el teorema anterior que dice que si la segunda derivada de una función es mayor que cero, entonces la función es convexa. Una función convexa siempre se curva hacia arriba, por lo que podemos concluir que la función f (x) = 3x^2 + 7x – 9 es convexa y se curva hacia arriba.

Identifica la curva de la siguiente función y determina si es una función cóncava o convexa:

f (x) = -9x^2 – x – 1

Solución

En primer lugar, calcularemos la primera derivada de la función empleando las reglas de suma/diferencia y potencia de la diferenciación:

f ‘ (x) = -18x – 1

Ahora diferenciaremos la primera derivada para calcular la segunda derivada de la función:

f » (x) = -18

Ahora, compara los resultados con el teorema anterior que dice que si la segunda derivada de una función es menor que cero, entonces la función es cóncava. Una función cóncava siempre se curva hacia arriba, así que podemos concluir que la función f (x) = -9x^2 – x – 1 es cóncava y se curva hacia abajo.

Vídeos de Convexo y cóncavo

Contenido