Cotangente
La cotangente es una de las razones trigonométricas básicas. De hecho, es una de las razones trigonométricas recíprocas csc, sec y cot. Se suele denotar como «cot x», donde x es el ángulo entre la base y la hipotenusa de un triángulo rectángulo. Los nombres alternativos de la cotangente son cotan y cotangente x. La cotangente de un ángulo en un triángulo rectángulo se define como el cociente entre el lado adyacente (el lado adyacente al ángulo) y el lado opuesto (el lado opuesto al ángulo).
Fórmula de la cotangente
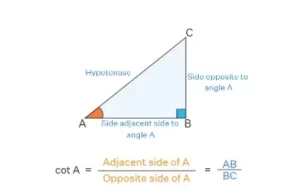
La fórmula de la cotangente para un ángulo θ es: cot θ = (Lado adyacente) / (Lado opuesto). Veamos el triángulo rectángulo ABC que forma un ángulo recto con B. Entonces AB es el lado adyacente a A y BC es el lado opuesto a A. Entonces la cotangente de A (que se escribe como cot A) es
cot A = (Lado adyacente de A) / (Lado opuesto de A) = (AB) / (BC).
Propiedades de la cotangente
Ya sabemos que cot x = (Adyacente) / (Opuesto). Aparte de esto, hay varias otras fórmulas de la razón cotangente en las que la cotangente se puede escribir en términos de otras razones trigonométricas.
Cotangente en términos de Cos y Sin
Sabemos que sin θ = (Opuesto) / (Hipotenusa) y cos θ = (Adyacente) / (Hipotenusa). Si dividimos cos θ entre sin θ , obtenemos
(cos θ) / (sin θ) = (Adyacente) / (Hipotenusa) × (Hipotenusa) / (Opuesta)
= (Adyacente) / (Opuesto)
= cot θ
Por lo tanto, cot θ = (cos θ) / (sin θ) es la fórmula de cot x en términos de cos y sin.
Cotangente en términos de Tan
Sabemos que tan θ = (Opuesto)/(Adyacente) y cot θ = (Adyacente)/(Opuesto). Por lo tanto, cot y tan son recíprocos entre sí. Así, podemos escribir cot θ = 1/tan θ y tan θ = 1/cot θ. Así, cot en términos de tan es. cot θ = 1/tan θ. Hay otra fórmula para escribir cot en términos de tan que es, cot θ = tan (π/2 – θ) (o) tan(90° – θ).
Cotangente en términos de Cosec
De una de las identidades pitagóricas, csc2θ – cot2θ = 1. De aquí obtenemos cot2θ = csc2θ – 1. Si sacamos raíz cuadrada a ambos lados, cot θ = √(csc2θ – 1). Por lo tanto, cot en términos de csc es, cot θ = √(csc2θ – 1)
Ley de la cotangente
Consideremos un triángulo ABC en el que AB = c, BC = a, y CA = b. La ley de la cotangente se parece a la ley del seno, pero implica a los medios ángulos. La ley de la cotangente dice: (cot A/2) / (s – a) = (cot B/2) / (s – b) = (cot C/2) / (s – c). Aquí, ‘s’ es el semiperímetro del triángulo, es decir, s = (a + b + c)/2.
Signo de la cotangente
La razón de la cotangente (por supuesto, tanto tan como cot) es positiva sólo en el primer y tercer cuadrante. Es negativa en el segundo y cuarto cuadrantes. Por lo tanto
cot (π – θ) = – cot θ (2º cuadrante)
cot (π + θ) = cot θ (3er cuadrante)
cot (2π – θ) = – cot θ (4º cuadrante)
cot (2π + θ) = cot θ (1er cuadrante)
Período de la cotangente
Sabemos que todas las funciones trigonométricas son funciones periódicas. Además, por el apartado anterior, sabemos que cot (2π + θ) = cot θ. Pero la función cotangente puede tener un periodo menor π (ya que la función cotangente es positiva en el primer y tercer cuadrante donde los ángulos del tercer cuadrante son π + el ángulo del primer cuadrante). Por tanto, el periodo de la cotangente es π, es decir, cot (π + θ) = cot θ.
Cotangente de un ángulo negativo
La cotangente de un ángulo negativo es el negativo de la cotangente de un ángulo positivo, es decir, cot (-x) = -cot x, para cualquier x en el dominio. De aquí podemos concluir que la cotangente es una función impar.
Cotangente en la circunferencia unitaria
Sabemos que cada punto de la circunferencia unitaria da los valores de cos y sin del ángulo correspondiente. Para hallar la cotangente del ángulo correspondiente, sólo tenemos que dividir el valor correspondiente de cos entre el valor correspondiente de sin porque tenemos la fórmula de cot x dada por, cot x = (cos x) / (sin x). Aquí podemos ver los valores de cot θ para algunos ángulos estándar.
Vídeos de Cotangente
Contenido