Ángulo entre dos rectas
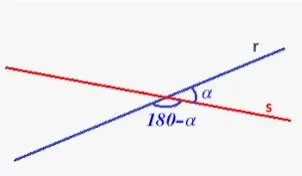
La relación entre dos líneas puede determinarse por el ángulo generado por las dos líneas. Lo que se calcula es el ángulo formado por las dos líneas. El ángulo agudo y el ángulo obtuso son dos ángulos formados por dos líneas que se cruzan. El ángulo formado por dos líneas se puede utilizar para calcular el ángulo formado por dos lados de un polígono cerrado. Veamos las fórmulas y los ejemplos para el ángulo formado por dos rectas en un plano de coordenadas, así como en el espacio tridimensional.El tema de las rectas es especialmente significativo en las matemáticas del IIT JEE. En concursos como el IIT JEE, suele dar lugar a preguntas sobre rectas. Dado que el tema es tan amplio, los estudiantes deben dedicar suficiente tiempo a la comprensión de los numerosos conceptos. En las rectas, el ángulo entre dos rectas es una cabeza importante.Cuando dos rectas se cruzan, se forman dos pares de ángulos. En la intersección se forman un par de ángulos agudos y otro par de ángulos obtusos. Los valores absolutos de los ángulos se determinan por las pendientes de las rectas que se cruzan.También cabe destacar que si una de las rectas se cruza con el eje y, no se puede determinar el ángulo generado por la intersección porque la pendiente de una recta paralela al eje y es ambigua.
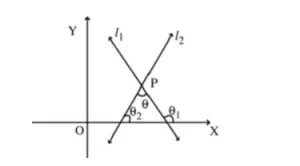
Sean L1 y L2 las dos rectas que se cruzan y supongamos que P es el punto de intersección de las dos rectas que hacen ángulo θ1 y θ2 con la dirección positiva del eje x.
L1: y = m1x + c1
L2: y = m2x + c2
m1 = tan θ1
m2 = tan θ2
Sea θ el ángulo entre las dos rectas.
θ1 = θ + θ2
θ = θ1 – θ2
tan θ = tan (θ1 – θ2)
Líneas paralelas
Si las dos rectas son paralelas, entonces sus pendientes son iguales.
m1 = m2
Si las rectas son paralelas, entonces los coeficientes de x e y son proporcionales en sus ecuaciones. En particular, las ecuaciones de dos rectas paralelas sólo se diferencian por el término constante.
Líneas perpendiculares
Si las dos rectas son perpendiculares, el producto de sus pendientes es -1.
1 + m1m2 = 0
m1m2 = -1
La ecuación de la recta perpendicular a la recta ax + by + c = 0 es de la forma bx – ay + k = 0 para algún k.
Vídeos de Ángulo entre dos rectas
Contenido