Operaciones con vectores
Un vector es una cantidad que tiene tanto una magnitud (o tamaño) como una dirección. Por ejemplo, la velocidad. La velocidad es una velocidad en una dirección determinada. Por tanto, aunque la velocidad es una cantidad escalar, ya que sólo tiene magnitud, la velocidad es un vector.
Un ejemplo de otra cantidad vectorial es el desplazamiento. Nos dice a qué distancia estamos de un punto fijo, y también nos dice nuestra dirección respecto a ese punto.
Ejemplos de otras cantidades vectoriales son: la aceleración debida a la gravedad de la tierra en un lugar determinado, la fuerza ejercida sobre un objeto.
Una cantidad escalar consta de magnitud, pero no de dirección. Ejemplos de magnitudes escalares son: distancia, velocidad, longitud, masa y tiempo.
Operaciones de álgebra vectorial
Al igual que en el Álgebra habitual, también realizamos operaciones aritméticas como la suma, la resta y la multiplicación sobre vectores. Sin embargo, en el caso de la multiplicación, los vectores tienen dos terminologías, como producto punto y producto cruz.
Suma de vectores
Consideremos que hay dos vectores P y Q, entonces la suma de estos dos vectores se puede realizar cuando la cola del vector Q se encuentra con la cabeza del vector A. Y durante esta suma, la magnitud y la dirección de los vectores no deben cambiar. La suma de vectores sigue dos leyes importantes, que son
Ley conmutativa: P + Q = Q + P
Ley Asociativa: P + (Q + R) = (P + Q) + R
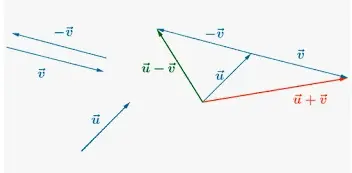
Sustracción de vectores
Aquí se invierte el sentido de los otros vectores y se realiza la suma de ambos vectores. Si P y Q son los vectores, para los cuales el método de la resta tiene que ser realizado, entonces invertimos la dirección de otro vector digamos para Q, lo hacemos -Q. Ahora, tenemos que sumar los vectores P y -Q. Así, la dirección de los vectores es opuesta, pero la magnitud sigue siendo la misma.
P – Q = P + (-Q)
Multiplicación de vectores
Si k es una cantidad escalar y se multiplica por un vector A, la multiplicación escalar viene dada por kA. Si k es positivo, entonces la dirección del vector kA es la misma que la del vector A, pero si el valor de k es negativo, entonces la dirección del vector kA será opuesta a la del vector A. Y la magnitud del vector kA viene dada por |kA|.
Producto punto
El producto punto es a menudo llamado producto escalar. Se representa utilizando un punto(.) entre dos vectores. En este caso, dos vectores de coordenadas de igual longitud se multiplican de tal manera que dan como resultado un único número. Así que, básicamente, cuando tomamos el producto escalar de dos vectores, el resultado es un número o una cantidad escalar. Supongamos que P y Q son dos vectores, entonces el producto escalar de ambos vectores viene dado por;
P.Q = |P| |Q| cos θ
Si P y Q están ambos en la misma dirección, es decir, θ = 0°, entonces
P.Q = |P| |Q|
Si P y Q son ambos ortogonales, es decir, θ = 90°, entonces
P.Q = 0 [ya que cos 90° = 0]
En el álgebra vectorial, si dos vectores están dados como;
P = [P1,P2,P3,P4,….,Pn] y Q = [Q1,Q2,Q3,Q4,….,Qn]
Entonces su producto punto viene dado por;
P.Q = P1Q1+P2Q2+P3Q3+……….PnQn
Vídeos de Operaciones con vectores
Contenido