Como se saca el apotema
En matemáticas, un polígono regular es un polígono con n lados, todos de igual longitud. Cada polígono regular tiene un radio, un apotema, un incirculo y un circuncirculo.
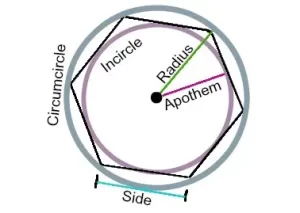
El radio de un polígono regular es la línea que une el centro del polígono con uno de sus vértices
La circunferencia es el círculo que rodea el exterior del polígono conectando todos sus vértices. El radio del polígono es también el radio de la circunferencia.
El incirculo es el círculo del interior del polígono que toca cada uno de los puntos medios de los lados.
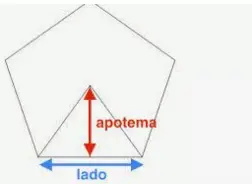
Por último, el apotema es la línea que une el centro del polígono con el punto medio de uno de sus lados. La apotema es también el radio del círculo interior.
Quizá te preguntes qué aspecto tendría la apotema en un polígono irregular, o en un polígono con lados de distinta longitud. Los polígonos irregulares no tienen punto central, por lo que no tienen apotema. Tiene sentido, ¿verdad? Los apotemas sólo se aplican a los polígonos regulares.
Cada uno de los polígonos regulares mostrados tiene un apotema. Un polígono regular de n lados siempre tiene un apotema, independientemente del número de lados que tenga. La longitud del apotema se puede utilizar para calcular otras características de un polígono.
Apotema y Área
El perímetro de un polígono regular es la distancia alrededor del polígono. Si conocemos la longitud de la apotema y el perímetro de un polígono regular, podemos calcular el área del polígono mediante la fórmula
A = (1/2)aP
donde a es la longitud de la apotema y P es el perímetro.
Por ejemplo, consideremos un polígono regular de 5 lados con una longitud de apotema de 4,817 unidades y un perímetro de 35 unidades. El área de este polígono se puede hallar introduciendo 4,817 para a y 35 para P en la fórmula para obtener
A = (1/2)(4,817)(35) = 84,2975 unidades cuadradas
El área de este polígono es 84,2975 unidades cuadradas.
Más fórmulas
También podemos usar la fórmula del área para encontrar la apotema si conocemos tanto el área como el perímetro de un polígono. Esto se debe a que podemos resolver a en la fórmula, A = (1/2)aP, multiplicando ambos lados por 2 y dividiendo por P para obtener 2A / P = a.
Volvamos a la imagen del polígono regular de 5 lados y supongamos que, aunque no conocemos la apotema, sí sabemos que el área es de 84,2975 unidades cuadradas y el perímetro es de 35 unidades. Cuando introducimos estos números en la fórmula de la apotema, obtenemos
a = 2(84,2975) / 35 = 4,817 unidades
Aquí, el apotema tiene una longitud de 4,817 unidades.
A veces, no conocemos el área o el perímetro de un polígono regular de n lados. Cuando este es el caso, tenemos una fórmula que podemos utilizar para encontrar la longitud del apotema sabiendo sólo la longitud de un lado de un polígono. Cuando sólo conocemos la longitud de un lado, lo llamamos s de un polígono regular de n lados, y podemos utilizar la siguiente fórmula
a = s / (2tan(180 / n))
para hallar la longitud del apotema.
Vídeos de Como se saca el apotema
Contenido