Teorema de tales fórmula

por
Teorema de tales fórmula
El teorema de la proporcionalidad básica fue propuesto por un famoso matemático griego, Tales, de ahí que también se le conozca como teorema de Tales. Según el famoso matemático, para dos triángulos equiangulares cualesquiera, la razón de dos lados correspondientes de los triángulos dados es siempre la misma. A partir de este concepto, se propuso el teorema de la proporcionalidad básica (BPT). Este teorema proporciona la relación entre los lados de dos triángulos equiangulares cualesquiera. En los triángulos semejantes se ha introducido el concepto del teorema de Tales. Si los dos triángulos dados son similares entre sí, entonces, Los ángulos correspondientes de ambos triángulos son iguales Los lados correspondientes de ambos triángulos son proporcionales entre sí. El teorema también nos ayuda a entender mejor el concepto de triángulos semejantes.

Teorema de tales fórmula

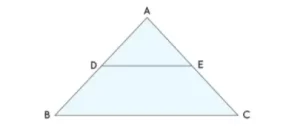
El teorema básico de la proporcionalidad, también conocido como teorema de Tales, afirma que «la línea trazada paralela a un lado de un triángulo y que corta a los otros dos lados divide a los otros dos lados en igual proporción». Por ejemplo, en la figura dada, la línea DE se traza paralela al lado BC, de forma que une los otros dos lados, AB y AC. Según el teorema básico de la proporcionalidad, se puede deducir que AD/DB = AE/EC.

Teorema de la proporcionalidad básica

Intentemos ahora demostrar el enunciado del teorema básico de proporcionalidad (BPT).

Enunciado: La recta trazada paralela a un lado de un triángulo y que corta a los otros dos lados, divide a los otros dos lados en igual proporción.

Dada: Consideremos un triángulo ΔABC, como se muestra en la figura dada. En este triángulo, trazamos una recta DE paralela al lado BC de ΔABC y que corta los lados AB y AC en D y E, respectivamente.

Construcción: En el diagrama anterior, crea líneas imaginarias donde puedas Unir C con D y B con E. Dibuja la perpendicular DP perpendicular a AE y EQ perpendicular a AD.

Prueba:

Consideremos los triángulos ADE y BDE. Estos dos triángulos tienen la misma base AB y la misma altura EQ.

(Área de ADE)/(Área de BDE) = (1/2 × AD × EQ)/(1/2 × BD × EQ)

(Área de ADE)/(Área de BDE) = AD/BD

Consideremos ahora los triángulos CDE y ADE. Ambos triángulos tienen la misma base AC y la misma altura DP.

(Área de ADE)/(Área de CDE) = (1/2 × AE × DP)/(1/2 × CE × DP)

(Área de ADE)/(Área de CDE) = AE/CE

Los dos triángulos BDE y CDE están entre el mismo conjunto de rectas paralelas.

Área del triángulo BDE = Área del triángulo CDE

Aplicando esto tenemos, (Área del triángulo ADE)/(Área del triángulo BDE) = (Área del triángulo ADE)/(Área del triángulo CDE)

AD/BD = AE/CE

Corolario:

La demostración anterior también sirve para demostrar otro teorema importante llamado teorema del punto medio. El teorema del punto medio afirma que un segmento de línea trazado paralelamente a un lado de un triángulo y a la mitad de ese lado divide a los otros dos lados en los puntos medios.

Conclusión:

Por lo tanto, demostramos el Teorema de la Proporcionalidad Básica. Por tanto, la recta DE trazada paralela al lado BC del triángulo ABC divide a los otros dos lados AB, AC en igual proporción. Además, la inversa del BPT, teorema del punto medio, también es cierta. Afirma que la línea trazada por el punto medio de un lado de un triángulo que es paralela a otro lado biseca el tercer lado del triángulo

Vídeos de Teorema de tales fórmula

https://www.youtube.com/watch?v=eoSvj4BbC7U

Contenido