Semejanza de triángulos
Los triángulos semejantes son los triángulos que se parecen entre sí, pero sus tamaños pueden no ser exactamente iguales. Se puede decir que dos objetos son similares si tienen la misma forma pero pueden variar de tamaño. Esto significa que las formas similares se superponen entre sí cuando se amplían o desagregan. Esta propiedad de las formas similares se denomina «Similitud».
Definición de triángulos semejantes
Dos triángulos serán semejantes si los ángulos son iguales (ángulos correspondientes) y los lados están en la misma relación o proporción (lados correspondientes). Los triángulos semejantes pueden tener diferentes longitudes individuales de los lados de los triángulos, pero sus ángulos deben ser iguales y su correspondiente proporción de la longitud de los lados debe ser la misma. Si dos triángulos son semejantes significa que
- Todos los pares de ángulos correspondientes de los triángulos son iguales.
- Todos los lados correspondientes de los triángulos son proporcionales.
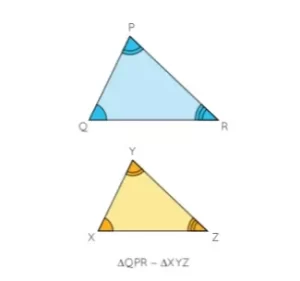
Utilizamos el símbolo «∼» para representar la similitud. Así, si dos triángulos son semejantes, lo mostramos como △QPR ∼ △XYZ
Ejemplos de triángulos semejantes
Los triángulos semejantes son triángulos cuyos pares de ángulos correspondientes son iguales. Esto significa que los triángulos equiangulares son semejantes. Por lo tanto, todos los triángulos equiláteros son ejemplos de triángulos semejantes. La siguiente imagen muestra triángulos semejantes, pero debemos observar que sus tamaños son diferentes.
Fórmulas de triángulos semejantes
En el apartado anterior hemos visto que hay dos condiciones con las que podemos comprobar si el conjunto de triángulos dado es semejante o no. Estas condiciones establecen que dos triángulos pueden decirse semejantes si sus ángulos correspondientes son iguales o congruentes o si sus lados correspondientes están en proporción. Por lo tanto, dos triángulos △ABC y △EFG pueden demostrarse semejantes(△ABC ∼ △EFG) utilizando cualquiera de las dos condiciones entre el siguiente conjunto de fórmulas de triángulos semejantes,
Fórmula de los triángulos semejantes en geometría:
∠A = ∠E, ∠B = ∠F y ∠C = ∠G
AB/EF = BC/FG = AC/EG
Teoremas de los triángulos semejantes
Podemos averiguar o demostrar si dos triángulos son semejantes o no utilizando los teoremas de semejanza. Utilizamos estos criterios de semejanza cuando no tenemos la medida de todos los lados del triángulo o la medida de todos los ángulos del triángulo. Estos teoremas de los triángulos semejantes nos ayudan a averiguar rápidamente si dos triángulos son semejantes o no. Hay tres tipos principales de reglas de semejanza, como se indica a continuación,
- AA (o AAA) o teorema de semejanza ángulo-ángulo
- SAS o Teorema de similitud lado-ángulo-lado
- SSS o Teorema de similitud lado-lado-lado
Vídeos de Semejanza de triángulos
Contenido