Triangulo equilátero
Como ya hemos comentado en la introducción, un triángulo equilátero es un triángulo que tiene todos sus lados de igual longitud. Además, los tres ángulos del triángulo equilátero son congruentes e iguales a 60 grados. La suma de los tres ángulos de un triángulo equilátero es igual a 180 grados. 60° + 60° + 60° = 180°. Por tanto, obedece a la propiedad de la suma de ángulos del triángulo.
Forma del triángulo equilátero
La forma de un triángulo equilátero es regular. La palabra «Equilátero» está formada por la combinación de dos palabras, es decir, «Equi» que significa igual y «Lateral» que significa lados. Un triángulo equilátero también se llama polígono regular o triángulo regular porque todos sus lados son iguales.
Supongamos que ABC es un triángulo equilátero, entonces, según la definición
AB = BC = AC, donde AB, BC y AC son los lados del triángulo equilátero.
Y
∠A = ∠B = ∠C = 60°.
En función de los lados hay otros dos tipos de triángulos:
- Triángulo escaleno
- Triángulo isósceles
Propiedades del triángulo equilátero
- Los tres lados son iguales.
- Los tres ángulos son congruentes y son iguales a 60 grados.
- Es un polígono regular de tres lados.
La perpendicular trazada desde el vértice del triángulo equilátero al lado opuesto lo divide en mitades iguales. También el ángulo del vértice desde el que se traza la perpendicular se divide en dos ángulos iguales, es decir, de 30 grados cada uno.
- El ortocentro y el centroide están en el mismo punto.
- En un triángulo equilátero, la mediana, la bisectriz del ángulo y la altitud de todos los lados son iguales.
- El área de un triángulo equilátero es √3a2/ 4
- El perímetro de un triángulo equilátero es 3a.
Teorema del triángulo equilátero
Si ABC es un triángulo equilátero y P es un punto del arco BC de la circunferencia del triángulo ABC, entonces;
PA = PB + PC
Demostración: Para un cuadrilátero cíclico ABPC, tenemos;
PA⋅BC=PB⋅AC+PC⋅AB
Como sabemos, para un triángulo equilátero ABC
AB = BC = AC
Por lo tanto
PA.AB = PB.AB+PC.AB
Tomando AB como común
PA.AB=AB(PB+PC)
PA = PB + PC
Por lo tanto, demostrado.
Fórmulas de triángulos equiláteros
Ya hemos entendido que un triángulo equilátero tiene los tres lados iguales en longitud y los tres ángulos iguales en medida. Ahora en base a estas propiedades se definen las fórmulas de los triángulos equiláteros. Las fórmulas más comunes que consideramos para un triángulo son
- Área del triángulo equilátero
- Perímetro del triángulo equilátero
- Altura del triángulo equilátero
Área del triángulo equilátero
El área de un triángulo equilátero es la región que ocupa en un plano bidimensional. La fórmula del área de un triángulo equiangular viene dada por:
A = √3a2/4
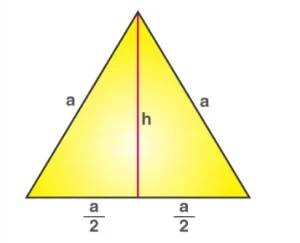
Si vemos la figura anterior, el área de un triángulo viene dada por;
Área = ½ x base x altura
Aquí Base = a y altura = h
Por lo tanto,
Área = ½ x a x h ………(1)
Ahora, a partir de la figura anterior, la altura h divide la base en mitades iguales, como a/2 y a/2. También forma dos triángulos rectángulos equivalentes.
Así, para un triángulo rectángulo, utilizando el teorema de Pitágoras, podemos escribir
a2 = h2 + (a/2)2
o
h2 = (a)2 – (a/2)2
= 3a2/4
h = √3a/2
Al poner este valor en la ecuación 1, obtenemos;
Área = ½ x a x √3a/2
A = √3a2/4
Por lo tanto, el área del triángulo equilátero es igual a √3a2/4.
Perímetro del triángulo equilátero
En geometría, el perímetro de cualquier polígono es igual a la longitud de sus lados. En el caso del triángulo equilátero, el perímetro será la suma de los tres lados.
Supongamos que ABC es un triángulo equilátero, entonces el perímetro de ∆ABC es;
Perímetro = AB + BC + AC
P = a + a + a
P = 3a
Donde a es la longitud de los lados del triángulo.
Altura del triángulo equilátero
La altura de un triángulo equilátero se puede determinar mediante el teorema de Pitágoras. También se llama altura de un triángulo equilátero. Como sabemos, un triángulo equilátero tiene todos los lados iguales. Ahora bien, si dejamos caer una altitud desde el vértice del triángulo hasta la base, ésta divide el triángulo en dos triángulos rectángulos iguales.
Así, a partir de la figura anterior, podemos encontrar la altura (h) del triángulo equilátero, como
h = √3a/2
Donde a es el lado del triángulo.
Así, para resumir las fórmulas relacionadas con el triángulo equilátero son:
- Área √3a2/4
- Perímetro 3a
- Altura √3a/2
Centroide del triángulo equilátero
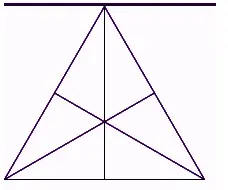
El centroide del triángulo equilátero se encuentra en el centro del triángulo. Dado que todos sus lados son iguales en longitud, es fácil encontrar el centroide para él.
Para encontrar el centroide, tenemos que trazar perpendiculares desde cada vértice del triángulo a los lados opuestos. Estas perpendiculares son todas de igual longitud y se cruzan en un único punto, que se conoce como centroide. Mira la figura de abajo:
Vídeos de Triangulo equilátero
Contenido