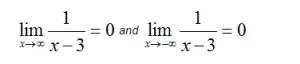Límites al infinito
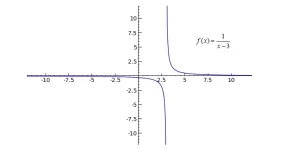
En esta gráfica, es bastante fácil ver que a medida que x se hace cada vez más grande o más pequeña, el valor y de f(x) se acerca mucho a cero, aunque nunca llega a ser realmente igual a cero. Cuando la curva de una función sugiere una línea invisible en un determinado valor de y (como en y=0 en esta gráfica), se dice que tiene una asíntota horizontal en ese valor de y. Podemos usar límites para describir el comportamiento de la asíntota horizontal en esta gráfica, como:
Prueba a poner xmín como -100 y xmáx como 100, y verás que f(x) se acerca mucho a cero cuando x es muy grande o muy pequeño. Que es lo que deberías esperar, ya que uno dividido por un número grande producirá naturalmente un resultado pequeño.
El concepto de límites unilaterales se puede aplicar a la asíntota vertical en este ejemplo, ya que se puede ver que a medida que x se acerca a 3 por la izquierda, la función se acerca al infinito negativo, y que a medida que x se acerca a 3 por la derecha, la función se acerca al infinito positivo, o:
Desgraciadamente, el comportamiento de las funciones a medida que x se acerca al infinito positivo o negativo no siempre es tan fácil de describir. Si alguna vez te encuentras con un caso en el que no puedes discernir el comportamiento de una función en el infinito, ya sea porque no hay una gráfica disponible o porque no está muy clara, imaginar qué tipo de valores se producirían cuando se sustituye x por diez mil o cien mil normalmente te dará una buena indicación de lo que hace la función cuando x se acerca al infinito.
Vídeos de Límites al infinito
Contenido