Formula del seno
Tomemos un triángulo oblicuo, es decir, un triángulo sin ángulo recto. Por lo tanto, es un triángulo cuyos ángulos son todos agudos o un triángulo con un ángulo obtuso. Es muy útil para resolver la información que falta en un triángulo dado.
Por ejemplo, si se conocen los tres lados del triángulo, la fórmula del seno nos permitirá encontrar cualquiera de sus tres ángulos o todos ellos. Del mismo modo, si se conocen dos lados y el ángulo entre estos dos lados, entonces la fórmula del seno nos permite encontrar la longitud del tercer lado.
La ley del seno
La regla del seno se utiliza en los siguientes casos
CASO-1: Dados dos ángulos y un lado en triángulo, es decir, AAS o ASA.
CASO-2: Dados dos lados y un ángulo no incluido en el triángulo, es decir, SSA
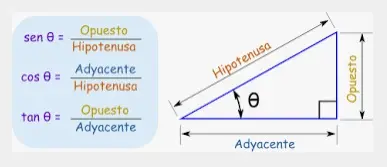
Para calcular el ángulo del triángulo rectángulo se utiliza la fórmula del seno. La relación entre los lados y los ángulos del ángulo recto se muestra a través de esta fórmula. El seno es la relación entre el lado opuesto y el lado de la hipotenusa del triángulo rectángulo. El lado más largo es la hipotenusa y el lado opuesto a la hipotenusa es el lado opuesto. En trigonometría, Sin es la abreviatura de la función seno.
Fórmula del ángulo seno
La fórmula del ángulo seno es,
Ejemplos resueltos
- Calcular el ángulo seno de un triángulo rectángulo cuyo lado opuesto e hipotenusa son 10 cm y 12 cm respectivamente?
Solución:
Dado, Lado opuesto = 10 cm Hipotenusa = 12 cm
Utilizando la fórmula
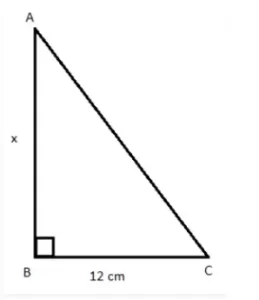
- Si sen A = 0,5, encuentra el valor de x en la siguiente figura.
Solución:
Dada,
Sin A = 0,5 = 5/10 = ½
Sabemos que sin θ = Opuesto/Hipotenusa
BC/AC = ½
12/AC = ½
AC = 12 × 2 = 24 cm
Por el teorema de Pitágoras
AC2 = AB2 + BC2
242 = x2 + 122
x2 = 576 – 144
x2 = 432
x = √452 cm
x=20,78 cm
Vídeos de Formula del seno
Contenido