Volumen de una pirámide cuadrangular
La fórmula del volumen de una pirámide viene dada por,
El volumen de una pirámide rectangular se define como el espacio tridimensional que ocupa esta figura. Podemos calcular el valor de este volumen multiplicando el área de la base por la altura de la pirámide y dividiendo por tres. Esto significa que necesitamos tres longitudes para calcular el volumen de estas pirámides, dos longitudes para la base y una longitud para la altura. Al tratarse de una medida tridimensional, el volumen se mide en unidades cúbicas como cm³, m³.
Ejemplo de Volumen de una pirámide cuadrangular
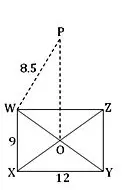
La base de una pirámide recta es un rectángulo de 12 metros de largo y 9 metros de ancho. Si cada una de las aristas inclinadas de la pirámide mide 8,5 metros, halla el volumen de la pirámide.
Solución:
Sea el rectángulo WXYZ la base de la pirámide derecha y sus diagonales WY y XZ se cruzan en O. Si OP es perpendicular al plano del rectángulo en O entonces OP es la altura de la pirámide derecha. Unir PW .
Ahora, desde el plano en ángulo recto ∆ WXY obtenemos,
WY² = WX² + XY²
o, WY² = 9² + 12²
o, WY² = 81 + 144
o, WY² = 225
o, WY = 15²
Por lo tanto, WY =15;
Por tanto, WO = 1/2 WY = 1/2 × 15 = 7,5
Como PO es perpendicular al plano del rectángulo WXYZ en O, por lo tanto PO ┴ OW
Por tanto, del triángulo rectángulo POW obtenemos
OW² + OP² = PW²
o bien, OP² = PW² – OW²
o bien, OP² = (8,5)² – (7,5)²
o, OP² = 16
o, OP = √16
Por lo tanto, OP = 4
es decir, la altura de la pirámide = 4 m.
Por tanto, el volumen necesario de la pirámide
= 1/3 × (área del rectángulo WXYZ) × OP
= 1/3 × 12 × 9 × 4 metros cúbicos
= 144 metros cúbicos.
Vídeos de Volumen de una pirámide cuadrangular
Contenido