Volumen cilindro
Un cilindro es una forma tridimensional con dos bases idénticas congruentes y paralelas. Hay diferentes tipos de cilindros. Son:
- Cilindro circular recto: Cilindro cuyas bases son círculos y cada segmento de línea que forma parte de la superficie curva lateral es perpendicular a las bases.
- Cilindro oblicuo: Cilindro cuyos lados se inclinan sobre la base en un ángulo que no es igual a un ángulo recto.
- Cilindro elíptico: Cilindro cuyas bases son elipses.
- Cilindro hueco circular recto: Cilindro formado por dos cilindros circulares rectos limitados uno dentro del otro.
¿Qué es el volumen de un cilindro?
El volumen de un cilindro es el número de cubos unitarios (cubos de longitud unitaria) que pueden caber en él. Es el espacio que ocupa el cilindro, como el volumen de cualquier forma tridimensional es el espacio que ocupa. El volumen de un cilindro se mide en unidades cúbicas como cm3, m3, in3, etc. Veamos la fórmula utilizada para calcular el volumen de un cilindro.
Definición de cilindro
Un cilindro es una forma sólida tridimensional que consta de dos bases paralelas unidas por una superficie curva. Estas bases son como un disco circular en una forma. La línea que pasa desde el centro o que une los centros de dos bases circulares se llama eje del cilindro.
Fórmula del volumen del cilindro
Sabemos que un cilindro se parece a un prisma (pero hay que tener en cuenta que un cilindro no es un prisma ya que tiene una cara lateral curva), utilizamos la misma fórmula del volumen de un prisma para calcular también el volumen de un cilindro. Sabemos que el área de un prisma se calcula mediante la fórmula
V = A × h, donde
A = área de la base
h = altura
Ahora aplicaremos esta fórmula para calcular el volumen de diferentes tipos de cilindros.
Volumen de un cilindro circular recto
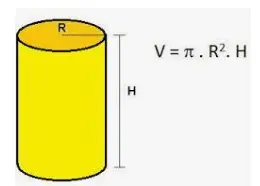
Sabemos que la base de un cilindro circular recto es un círculo y que el área de un círculo de radio ‘r’ es πr2. Por tanto, el volumen (V) de un cilindro circular recto, utilizando la fórmula anterior, es
V = πr2h
Aquí,
r es el radio de la base (círculo) del cilindro
h es la altura del cilindro
π es una constante cuyo valor es 22/7 (o) 3,142.
Por tanto, el volumen del cilindro varía directamente con su altura y varía directamente con el cuadrado de su radio, es decir, si el radio del cilindro se duplica, su volumen se cuadruplica.
Volumen de un cilindro oblicuo
La fórmula para calcular el volumen de un cilindro (oblicuo) es la misma que la de un cilindro circular recto. Así, el volumen (V) de un cilindro oblicuo cuyo radio de la base es ‘r’ y cuya altura es ‘h’ es
V = πr2h
Volumen de un cilindro elíptico
Sabemos que una elipse tiene dos radios. También sabemos que el área de una elipse cuyos radios son ‘a’ y ‘b’ es πab. Por tanto, el volumen de un cilindro elíptico es
V = πabh
Aquí,
‘a’ y ‘b’ son los radios de la base (elipse) del cilindro.
h’ es la altura del cilindro.
π es una constante cuyo valor es 22/7 (o) 3,142.
Volumen de un cilindro hueco circular recto
Como un cilindro circular recto es un cilindro formado por dos cilindros circulares rectos limitados uno dentro del otro, su volumen se obtiene restando el volumen del cilindro interior al del exterior. Así, el volumen (V) de un cilindro circular recto hueco es
V = π(R2 – r2)h
Aquí,
R’ es el radio de la base del cilindro exterior.
r’ es el radio de la base del cilindro interior.
h’ es la altura del cilindro.
π es una constante cuyo valor es 22/7 (o) 3,142.
Vídeos de Volumen cilindro
Contenido