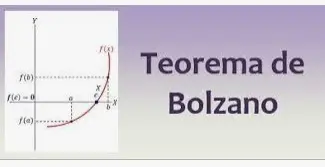
Teorema de bolzano
El teorema del valor intermedio afirma que si «f» es una función continua sobre un intervalo cerrado [a, b] cuyo dominio tiene valores f(a) y f(b) en los puntos extremos del intervalo, entonces la función toma cualquier valor entre los valores f(a) y f(b) en un punto dentro del intervalo. Este teorema se explica de dos maneras diferentes:
Teorema del valor intermedio
Enunciado 1:
Si k es un valor entre f(a) y f(b), es decir
f(a) < k < f(b) o f(a) > k > f(b)
entonces existe al menos un número c entre a y b, es decir, c ∈ (a, b) de forma que f(c) = k
Enunciado 2:
El conjunto de imágenes de la función en el intervalo [a, b], que contiene [f(a), f(b)] o [f(b), f(a)], es decir
o bien f([a, b]) ⊇ [f(a), f(b)] o bien f([a, b]) ⊇ [f(b), f(a)]
Explicación del teorema:
El enunciado del teorema del valor intermedio parece complicado. Pero se puede entender con palabras más sencillas. Consideremos el diagrama anterior, hay una función continua f con puntos extremos a y b, entonces la altura del punto «a» y «b» sería «f(a)» y «f(b)».
Si elegimos una altura k entre estas alturas f(a) y f(b), entonces, según este teorema, esta línea debe intersecar la función f en algún punto (digamos c), y este punto debe estar entre a y b.
Un teorema de valor intermedio, si c = 0, entonces se denomina teorema de Bolzano.
Demostración del teorema intermedio
Vamos a demostrar el primer caso del primer enunciado del teorema del valor intermedio ya que la demostración del segundo es similar.
Demostraremos este teorema mediante el uso de la propiedad de completitud de los números reales. La prueba de «f(a) < k < f(b)» se da a continuación:
Supongamos que A es el conjunto de todos los valores de x en el intervalo [a, b], de forma que f(x) ≤ k.
Aquí se supone que A es un conjunto no vacío ya que tiene un elemento «a» y además A está acotado por encima del valor «b».
Así, por la propiedad de completitud, tenemos que, «c» es el menor valor que es mayor o igual a cada elemento de A. Por lo tanto, podemos decir que f(c) = k.
Dado que f es continua. Entonces consideremos que a ε > 0, existe «a δ > 0» tal que
| f(x) – f(c) | < ε para todo | x – c | < δ. Esto nos da
f(x) – ε < f(c) < f(x) + ε
para cada x que se encuentre entre c – δ y c + δ. Por tanto, tenemos valores de x que se encuentran entre c y c -δ, contenidos en A, tales que :
f(c) < (f(x) + ε) ≤ (k + ε) — (1)
Análogamente, los valores de x entre c y c + δ que no están contenidos en A, tales que
f(c) > (f(x) – ε) > (k – ε) —(2)
Combinando ambas relaciones de desigualdad, se obtiene
k – ε < f(c) < k + ε
Para todo ε > 0
Por lo tanto, el teorema queda demostrado.
Aplicaciones del teorema intermedio
El teorema del valor intermedio tiene muchas aplicaciones. Matemáticamente, se utiliza en muchas áreas. Este teorema se utiliza para demostrar que existe un punto por debajo o por encima de una determinada recta. También se utiliza para analizar la continuidad de una función que es continua o no.
Este teorema también tiene muchas implicaciones en problemas de Física y Química. Es aplicable siempre que haya una cantidad escalar que varíe continuamente y cuyos puntos extremos compartan el mismo valor de una variable. Estas cantidades pueden ser: presión, temperatura, elevación, concentración de gas carbónico, etc.
El teorema del valor intermedio tiene también algunas aplicaciones importantes en la vida real. Tomemos el ejemplo de una mesa que se tambalea debido al desnivel del suelo. Para solucionarlo, gire la mesa, siempre que el suelo sea continuo, es decir, que no haya altibajos debidos a baldosas mal colocadas.
La mesa que se tambalea tendrá tres de sus patas tocando el suelo, mientras que su cuarta pata será el problema. Al girar la mesa en un punto, la cuarta pata estará por debajo del suelo, y en otro punto, estará por encima del suelo. Según el teorema del valor intermedio, habrá un punto en el que la cuarta pata tocará perfectamente el suelo, y la mesa estará fija.
Vídeos de Teorema de bolzano
Contenido