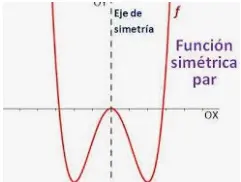
Funciones simetricas
Por ejemplo, x^2+y^2+z^2x
2 +y 2 +z 2
es un polinomio simétrico, ya que cambiando cualquier par, digamos xx e yy, el polinomio resultante y^2+x^2+z^2y
2 +x 2 +z 2
es el mismo que el polinomio inicial. Los polinomios simétricos se encuentran a menudo en la fórmula de Vieta y en las identidades de Newton.
Función que no cambia bajo ninguna permutación de sus variables independientes. Los siguientes son ejemplos de funciones simétricas: x1+⋯+xn, x1⋯xn,
∑1≤i<j≤nxixj, max(x1,…,xn),
x1+⋯+xn(modm),
la suma en notación decimal de un conjunto arbitrario de números de un dígito, una «función de votación» , que se caracteriza porque sus variables independientes toman sólo dos valores 1 («a favor» ) y 0 («en contra» ), y la propia función se pone igual a 1 si más de la mitad de sus variables independientes son 1 y se pone igual a 0 en caso contrario. Ejemplos triviales de funciones simétricas son las funciones constantes y la función de una variable.
Cualquier función simétrica no constante depende esencialmente de todas sus variables. Así, la adición de variables no esenciales que no sean constantes hace que una función no sea simétrica, y su eliminación puede hacerla simétrica. Así, el concepto de función simétrica depende de la indicación exacta de todas sus variables. Un criterio sencillo para la simetría de una función f(x1,…,xn) es que se cumplan simultáneamente las dos ecuaciones siguientes
f(x1,x2,x3,…,xn)= f(x2,x1,x3,…,xn),
f(x1,x2,x3,…,xn)=f(xn,x1,x2,…,xn-1)
o, lo que es lo mismo, que se cumplan n-1 de las siguientes ecuaciones
f(x1,…,xi,xi+1,…,xn)= f(x1,…,xi+1,xi,…,xn),
junto con
f(x1,x2,…,xn-1,xn)= f(xn,x2,…,xn-1,x1).
Las funciones simétricas están relacionadas con los polinomios simétricos. Toda función simétrica racional (sobre un campo de característica 0) es el cociente de dos polinomios simétricos. Toda función simétrica booleana toma valores iguales en conjuntos de sus argumentos que contienen igual número de identidades. Estas funciones desempeñan un papel importante en la cibernética matemática y sus aplicaciones y, en particular, aparecen en la realización esquemática de operaciones aritméticas y de otro tipo.
Vídeos de Funciones simetricas
Contenido