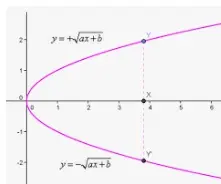
Función radical
Un radical es una raíz de un número, que puede ser una raíz cuadrada, una raíz cúbica, etc. Una raíz cuadrada también se llama radical. Una función radical es cualquier función que se define en una raíz. Esta función también contiene una raíz cuadrada, raíces cúbicas, o cualquier raíz enésima.
Una función radical es cualquier función que contiene una variable dentro de una raíz. Esto incluye raíces cuadradas, raíces cúbicas o cualquier raíz enésima.
Ejemplos: y=√(x+3)
p= √ (3q)+17
f(x)=∜ (x-z)
Esto no incluye las funciones que sólo contienen números dentro de los radicales. Una variable independiente debe estar dentro del radical.
Ejemplos de funciones no radicales: f(x)=x+√2
y=x^2+3x+√5
¿Cómo se resuelven las ecuaciones radicales?
Unos sencillos pasos pueden ayudarte a resolver una función para un valor dado.
- Para ello, primero se aísla el radical en un lado de la ecuación.
- Luego se llevan ambos lados de la ecuación a la misma potencia de la raíz. (Por ejemplo, si hay una raíz cuadrada, se eleva al cuadrado ambos lados).
- Esto eliminará la raíz y dejará todo lo que hay dentro de ella sin tocar. (por ejemplo, (√ x)^2=x ).
- Entonces la ecuación restante debería ser fácil de resolver usando álgebra básica.
Ejemplo 1: 2=√ (3q)+17
Primero aísla el radical restando 17 de ambos lados.
2-17=√ (3q)+17-17
-15=√ (3q)
Luego eleva al cuadrado ambos lados.
(-15)^2=[√ (3q)]^2
225=3q
Entonces resuelve para q dividiendo ambos lados entre 3.
225/3=3q/3
Simplifica.
q=75
Ejemplo 2: 3=∜(x-5)
Como la raíz ya está aislada, podemos simplemente llevar ambos lados a la cuarta potencia.
3^4=[∜(x-5)]^4
81=x-5
De nuevo resolvemos para x.
x=86
Rango de las funciones de raíz cuadrada
Un concepto relacionado con el dominio de una función es su rango. Mientras que el dominio de una función son todos los valores de x que son válidos dentro de la función, su rango son todos los valores de y en los que la función es válida. Esto significa que el rango de una función es igual a todas las salidas válidas de esa función. Esto se puede calcular estableciendo y igual a la propia función, y luego resolviendo para encontrar cualquier valor que no sea válido.
En el caso de las funciones de raíz cuadrada, esto significa que el rango de la función son todos los valores producidos cuando x resulta en un radicando que es igual o mayor que cero. Calcula el dominio de tu función de raíz cuadrada, y luego introduce el valor de tu dominio en la función para determinar el rango. Si tu función es
f(x) = \sqrt{x – 2}
y calculas el dominio como todos los valores de x mayores o iguales a 2, entonces cualquier valor válido que pongas en
y = \sqrt{x – 2}
le dará un resultado que es mayor o igual a cero. Por lo tanto, su rango es y ≥ 0 o [0, ∞).
Vídeos de Función radical
Contenido