Funcion identidad
Se considera que una función es una función identidad cuando devuelve el mismo valor que la salida que se utilizó como entrada. Sigamos adelante y aprendamos la definición de una función de identidad.
Definición de Función Identidad
Una función identidad es una función en la que cada elemento de un conjunto B da la imagen de sí mismo como el mismo elemento es decir, g (b) = b ∀ b ∈ B. Por lo tanto, es de la forma g(x) = x y se denota por «I». Se llama función identidad porque la imagen de un elemento en el dominio es idéntica a la salida en el rango. Así, una función identidad mapea cada número real a sí mismo. La salida de una función identidad es la misma que su entrada. Las funciones de identidad pueden identificarse fácilmente ya que la preimagen y la imagen son idénticas.
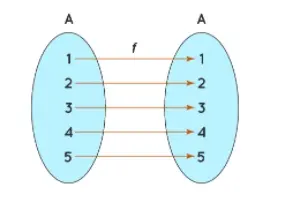
Consideremos un ejemplo de una función que mapea elementos del conjunto A = {1, 2, 3, 4, 5} a sí mismo. g: A → A tal que, g = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5)}.
A partir de la imagen anterior, podemos ver que la función f es una función de identidad, ya que cada elemento de A se mapea sobre sí mismo. La función f es unívoca y onto.
Dominio, rango e inversa de la función identidad
Una función identidad es una función de valor real que puede representarse como g: R → R tal que g(x) = x, para cada x ∈ R. Aquí, R es un conjunto de números reales que es el dominio de la función g. El dominio y el rango de las funciones identidad son los mismos. Si la entrada es √5, la salida es también √5; si la entrada es 0, la salida es también 0.
- El dominio de la función identidad g(x) es R
- El rango de la función identidad g(x) es también R
El codominio y el rango de una función identidad son conjuntos iguales. ⇒ La función identidad es onto.
La inversa de cualquier función intercambia el dominio y el rango de esa función. Esto implica que la función identidad es invertible y es su propia inversa.
Gráfica de la función identidad
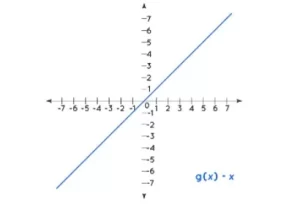
Para representar la gráfica de una función identidad, podemos representar los valores de las coordenadas x en el eje x y los valores de las coordenadas y en el eje y. La gráfica de una función identidad es una recta que pasa por el origen. Para una función identidad, el dominio y el rango son los mismos.
Podemos ver en la gráfica anterior que la recta forma un ángulo de 45° con el eje x y el eje y. La pendiente de la gráfica de la función identidad siempre es 1.
Propiedades de la función identidad
Las funciones identidad se utilizan principalmente para devolver el valor exacto de los argumentos sin cambiar en una función. Una función identidad no debe confundirse con una función nula o una función vacía. Estas son las propiedades importantes de una función identidad:
- La función identidad es una función lineal de valor real.
- La gráfica de una función identidad subtiende un ángulo de 45º con el eje x y el eje y.
- Como la función es biyectiva, es la inversa de sí misma.
- La gráfica de una función identidad y su inversa son iguales.
Vídeos de Funcion identidad
Contenido