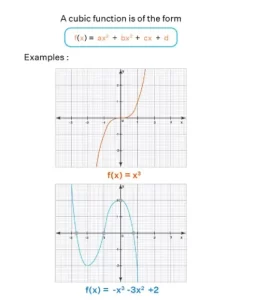
Funcion cubica
Una función cúbica es una función algebraica.
Dominio y rango de la función cúbica
Como una función cúbica y = f(x) es una función polinómica, está definida para todos los valores reales de x y, por tanto, su dominio es el conjunto de todos los números reales (R). Además, si observas los dos ejemplos (en la figura anterior), todos los valores de y están siendo cubiertos por la gráfica, y por lo tanto el rango de una función cúbica es el conjunto de todos los números también. Por tanto, concluimos que
- El dominio de una función cúbica es R.
- El rango de una función cúbica es R.
Asíntotas de la función cúbica
Las asíntotas corresponden siempre a los valores que se excluyen del dominio y del rango. Dado que tanto el dominio como el rango de una función cúbica es el conjunto de todos los números reales, ningún valor queda excluido ni del dominio ni del rango. Por lo tanto, una función cúbica no tiene asíntotas verticales ni tiene asíntotas horizontales.
Interceptos de una función cúbica
Como sabemos, hay dos tipos de interceptos de una función: la(s) intersección(es) en x y la(s) intersección(es) en y. Veamos cómo encontrar los interceptos de una función cúbica.
Intercepto X de una función cúbica
Los interceptos x de una función se conocen también como raíces (o) ceros. Como el grado de una función cúbica es 3, puede tener un máximo de 3 raíces. Como las raíces complejas de cualquier función siempre se dan en pares, una función siempre tendrá 0, 2, 4, … raíces complejas. Así que una función puede tener 0 o dos raíces complejas. Por lo tanto, tiene una o tres raíces reales o intersecciones x. Para hallar la(s) intersección(es) de una función cúbica, basta con sustituir y = 0 (o f(x) = 0) y resolver los valores de x.
Para encontrar la(s) intersección(es) de f(x) = x3 – 4×2 + x – 4, sustituye f(x) = 0. Entonces
x3 – 4×2 + x – 4 = 0
x2 (x – 4) + 1 (x – 4) = 0
(x – 4) (x2 + 1) = 0
x – 4 = 0; x2 + 1 = 0
x = 4 ; x2 = -1
x = 4 ; x = ± i
Los números complejos no pueden ser los intersticios de x. Por tanto, f(x) sólo tiene una intersección en x que es (4, 0).
Vídeos de Funcion cubica
Contenido