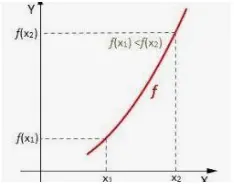
Función creciente
Las funciones crecientes y decrecientes son funciones cuyas gráficas van hacia arriba y hacia abajo, respectivamente, a medida que nos desplazamos hacia el lado derecho del eje x. Las funciones crecientes y decrecientes también se denominan funciones no decrecientes y no crecientes.
Definición de funciones crecientes y decrecientes
- Función creciente – Se dice que una función f(x) es creciente en un intervalo I si para cualesquiera dos números x e y en I tales que x < y, tenemos f(x) ≤ f(y).
- Función decreciente – Se dice que una función f(x) es decreciente en un intervalo I si para cualesquiera dos números x e y en I tales que x < y, tenemos f(x) ≥ f(y).
- Función estrictamente creciente – Se dice que una función f(x) es estrictamente creciente en un intervalo I si para cualesquiera dos números x e y en I tales que x < y, tenemos f(x) < f(y).
- Función estrictamente decreciente – Se dice que una función f(x) es estrictamente decreciente en un intervalo I si para cualesquiera dos números x e y en I tales que x < y, tenemos f(x) > f(y).
Representación gráfica de funciones crecientes y decrecientes
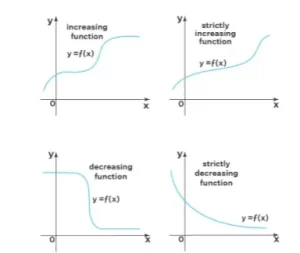
Ahora que conocemos el significado y la definición de las funciones crecientes y decrecientes, vamos a ver la representación gráfica de las funciones crecientes y decrecientes que nos ayudará a entender el comportamiento de las funciones.
Las gráficas anteriores muestran la representación gráfica de funciones estrictamente crecientes, estrictamente decrecientes, crecientes y decrecientes. Como podemos ver en los gráficos, la función creciente contiene tanto intervalos estrictamente crecientes como intervalos en los que la función es constante. Del mismo modo, una función decreciente consta de intervalos en los que la función es estrictamente decreciente y en los que la función es constante.
Reglas para comprobar las funciones crecientes y decrecientes
Utilizamos la derivada de una función para comprobar si es una función creciente o decreciente. Supongamos que una función f(x) es diferenciable en un intervalo abierto I, entonces tenemos
Si f'(x) ≥ 0 en I, se dice que la función es creciente en I.
Si f'(x) ≤ 0 en I, se dice que la función es una función decreciente en I.
Ejemplo: Consideremos un ejemplo para entender mejor el concepto. Consideremos f(x) = x3 definida para todos los números reales. La derivada de f(x) = x3 viene dada por f'(x) = 3×2. Sabemos que el cuadrado de un número es siempre mayor o igual que 0, por lo tanto tenemos f'(x) = 3×2 ≥ 0 para todo x. Por lo tanto f(x) = x3 es una función creciente.
Propiedades de las funciones crecientes y decrecientes
Ya que sabemos cómo comprobar si una función es creciente o decreciente, repasemos las propiedades algebraicas de las funciones crecientes y decrecientes:
- Si las funciones f y g son funciones crecientes en un intervalo abierto I, entonces la suma de las funciones f + g también es creciente en este intervalo.
- Si las funciones f y g son funciones decrecientes en un intervalo abierto I, entonces la suma de las funciones f + g también es decreciente en este intervalo.
- Si la función f es una función creciente en un intervalo abierto I, entonces la función opuesta -f es decreciente en este intervalo.
- Si la función f es una función decreciente en un intervalo abierto I, entonces la función opuesta -f es creciente en este intervalo.
- Si la función f es una función creciente en un intervalo abierto I, entonces la función inversa 1/f es decreciente en este intervalo.
- Si la función f es una función decreciente en un intervalo abierto I, entonces la función inversa 1/f es creciente en este intervalo.
- Si las funciones f y g son funciones crecientes en un intervalo abierto I y f, g ≥ 0 en I, entonces el producto de las funciones fg es también creciente en este intervalo.
- Si las funciones f y g son funciones decrecientes en un intervalo abierto I y f, g ≥ 0 en I, entonces el producto de las funciones fg es también decreciente en este intervalo.
Vídeos de Función creciente
Contenido