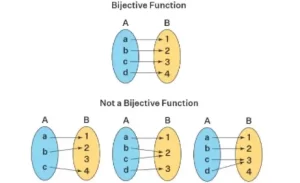
Funcion biyectiva
Una función biyectiva es una combinación de una función inyectiva y una función subjetiva. La función biyectiva relaciona elementos de dos conjuntos A y B con el dominio en el conjunto A y el codominio en el conjunto B, de forma que cada elemento de A está relacionado con un elemento distinto de B, y cada elemento del conjunto B es el codominio de algún elemento del conjunto A.
La función biyectiva es tanto una función unívoca como una función onto. Una función biyectiva del conjunto A al conjunto B tiene una función inversa del conjunto B al conjunto A. Una función biyectiva de un conjunto de elementos definidos a sí mismo se llama permutación. Aquí cada elemento del conjunto se relaciona consigo mismo.
De los ejemplos anteriores de función biyectiva, podemos observar que cada elemento del conjunto B ha sido relacionado con un elemento distinto del conjunto A. Las funciones no biyectivas tienen algún elemento en el conjunto B que no tiene una preimagen en el conjunto A, o alguno de los elementos del conjunto B es la imagen de más de un elemento del conjunto A.
Las funciones biyectivas deben satisfacer las cuatro condiciones siguientes.
- Cada elemento del conjunto A debe estar emparejado con un elemento del conjunto B.
- El elemento del conjunto A no debe estar emparejado con más de un elemento del conjunto B.
- Cada elemento del conjunto B debe estar emparejado con un elemento del conjunto A.
- El elemento del conjunto B no debe estar emparejado con más de un elemento del conjunto A.
Propiedades de la función biyectiva
A continuación se exponen algunas propiedades importantes de las funciones biyectivas.
- Los conjuntos dominio y codominio de una función biyectiva tienen igual número de elementos.
- El codominio y el rango de la función biyectiva son iguales.
- La función biyectiva tiene una función inversa.
- La función biyectiva no puede ser una función constante.
- La función biyectiva si se representa como una gráfica es siempre una recta.
- La función biyectiva sigue una propiedad reflexiva, simétrica y transitiva.
Ejemplo de función biyectiva
Demostrar que la función uno a uno f : {1, 2, 3} → {4, 5, 6} es una función biyectiva.
Solución:
La función dada f : {1, 2, 3} → {4, 5, 6} es una función unívoca, y por tanto relaciona cada elemento del dominio con un elemento distinto del conjunto codominio. Los tres elementos del conjunto del dominio se relacionan con los tres elementos del conjunto del codominio. Además, como el codominio incluye todos los elementos del segundo conjunto, la función dada es también una función onto.
Por lo tanto, la función dada es una función biyectiva.
Vídeos de Funcion biyectiva
https://www.youtube.com/watch?v=Qm_-dCWvHuI
Contenido