Bisectriz de un triangulo
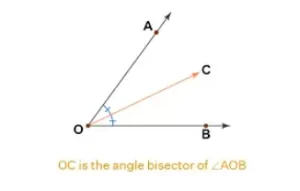
La bisectriz del ángulo en geometría es la semirrecta, línea o segmento que divide un ángulo dado en dos partes iguales. Por ejemplo, una bisectriz de un ángulo de 60 grados lo dividirá en dos ángulos de 30 grados cada uno. En otras palabras, divide un ángulo en dos ángulos congruentes más pequeños.
En un triángulo, la bisectriz de un ángulo es una línea recta que divide el ángulo en dos ángulos iguales o congruentes. En cada triángulo puede haber tres bisectrices de ángulos, una por cada vértice. El punto en el que confluyen estas tres bisectrices de ángulos en un triángulo se conoce como su incentro. La distancia entre el incentro y todos los vértices de un triángulo es la misma. Observa la siguiente imagen que muestra la bisectriz de un ángulo de un triángulo. Aquí, AG, CE y BD son las bisectrices de los ángulos ∠BAC, ∠ACB y ∠ABC respectivamente. F es el punto de intersección de las tres bisectrices que se conoce como incentro y está a igual distancia de cada uno de los vértices.
Propiedades de la bisectriz de un ángulo
Hasta ahora debes tener claro el significado de bisectriz de ángulo en geometría. Ahora, vamos a aprender algunas de las propiedades de la bisectriz de un ángulo que se enumeran a continuación:
Una bisectriz de un ángulo divide un ángulo en dos partes iguales.
Cualquier punto de la bisectriz de un ángulo es equidistante de los lados o brazos del ángulo.
En un triángulo, divide el lado opuesto en la proporción de la medida de los otros dos lados.
Construcción de la bisectriz de un ángulo
Pasos para construir una bisectriz de ángulo:
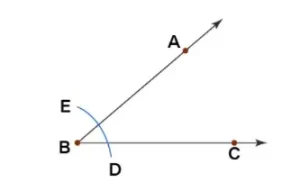
Paso 1: Dibujar un ángulo cualquiera, digamos ∠ABC.
Paso 2: Tomando B como centro y un radio cualquiera, dibuje un arco que interseque los rayos BA y BC en, digamos, E y D respectivamente.
Paso 3: Ahora, tomando D y E como centros y con el mismo radio que se tomó en el paso anterior, dibuje dos arcos para que se intersecten en F.
Paso 4: Une B con F y extiéndelo como una semirrecta. Esta semirrecta BF es la bisectriz del ángulo ABC.
Teorema de la bisectriz del ángulo
Entendamos ahora en detalle una importante propiedad de la bisectriz del ángulo de un triángulo como se ha dicho en el apartado anterior. Esta propiedad se conoce como el teorema de la bisectriz del ángulo de un triángulo. Según el teorema de la bisectriz del ángulo, en un triángulo, la bisectriz del ángulo trazada desde un vértice divide el lado sobre el que cae en la misma proporción que la de los otros dos lados del triángulo.
Afirmación: La bisectriz de un ángulo de un triángulo divide el lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo.
En la imagen anterior, PS es la bisectriz del ángulo de ∠P en ΔPQR. Por tanto, aplicando el teorema de la bisectriz del ángulo podemos decir que PQ/PR = QS/SR o a/b = x/y.
Vídeos de Bisectriz de un triangulo
Contenido