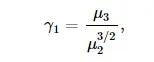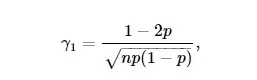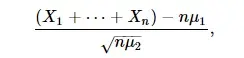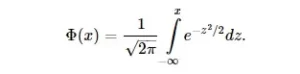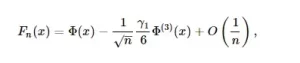Asimetria y curtosis
Los parámetros de asimetría y curtosis son medidas de la forma de la distribución. La asimetría (coeficiente de asimetría) da información sobre la tendencia de las desviaciones de la media a ser mayores en una dirección que en la otra. La asimetría es principalmente una descripción intuitiva de una distribución determinada. El tercer momento caracteriza la asimetría de una distribución.
La curtosis de una distribución de probabilidad de una variable aleatoria x se define como la relación entre el cuarto momento μ4 y el cuadrado de la varianza σ4.
donde μ2 y μ3 son el segundo y tercer momento central de la distribución, respectivamente. Para las distribuciones que son simétricas respecto a la expectativa matemática, γ1=0; según el signo de γ1 se habla de asimetría positiva ( γ1>0) y asimetría negativa ( γ1<0). En el caso de la distribución binomial correspondiente a n[[ Ensayos de Bernoulli|Ensayos de Bernoulli]] con probabilidad de éxito p,
se tiene: Si p=1/2(γ1=0), la distribución es simétrica; si p<1/2 o p>1/2, se obtienen diagramas de distribución típicos con una asimetría positiva (Fig.a) y negativa (Fig.b).
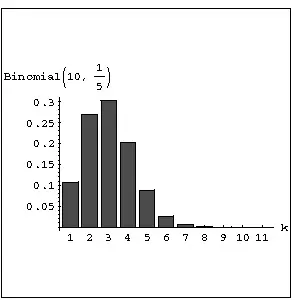
P(k,10,1/5). Diagrama de la distribución binomial P(k,n,p) correspondiente a n=10 ensayos Bernoulli, con asimetría positiva ( p=1/5 ).
P(k,10,4/5). Diagrama de la distribución binomial P(k,n,p) correspondiente a n=10 ensayos Bernoulli, con asimetría negativa ( p=4/5).
El coeficiente de asimetría (*) tiende a cero a medida que n→∞, de acuerdo con el hecho de que una distribución binomial normalizada converge a la distribución normal estándar.
El coeficiente de asimetría y el coeficiente de exceso son las características más utilizadas de la precisión con la que la función de distribución Fn(x) de la suma normalizada
donde X1…Xn se distribuyen idénticamente y son mutuamente independientes con un coeficiente de asimetría δ1, puede aproximarse mediante la función de distribución normal
En condiciones bastante generales, la serie de Edgeworth da como resultado
donde Φ(3)(x) es la derivada de orden tres.
Vídeos de Asimetria y curtosis
Contenido