Área de un trapecio rectángulo
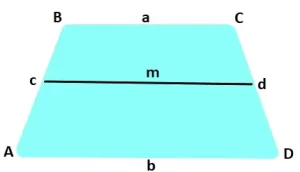
Si un círculo está inscrito en el trapecio, entonces la suma de los básicos siempre coincide con la suma de los lados: a + b = c + d, y la línea media siempre es igual a la mitad de la suma de los lados.
Un trapecio isósceles es un trapezoide cuyos lados son iguales a AB = CD. Entonces las diagonales AC = BD y los ángulos de la base son iguales:
De todos los trapezoides, sólo sobre un trapezoide isósceles se puede describir una circunferencia si la suma de los ángulos rectos opuestos es 180 °. En un trapezoide isósceles, la distancia desde la parte superior de una base a la proyección de la parte superior opuesta, que está directamente conectada a la base, es siempre precisamente la línea central.
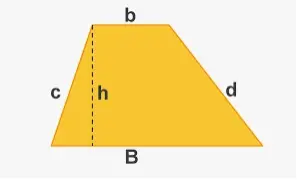
Un trapezoide rectangular es un tipo de trapezoide que contiene un ángulo de base de 90 °.
Teorema: Área del trapecio
Para calcular el área de un polígono arbitrario, hacemos lo siguiente: dividimos el polígono en triángulos y hallamos el área de un triángulo. La suma de las áreas de estos triángulos es igual al área del polígono. Utilizando esta técnica, obtenemos una fórmula para calcular el área que sobra del trapecio. Convengamos en llamar altura de un trapezoide a la perpendicular trazada desde cualquier punto de una de las bases a una recta que contenga otra base. En la figura siguiente, hemos indicado que el segmento de recta BH es la altura del trapecio ABCD:
Basándonos en esto, obtenemos el teorema «El área de un trapecio es igual al producto de la semisuma de sus bases y la altura». Basándonos en la fórmula del área, podemos demostrar este teorema.
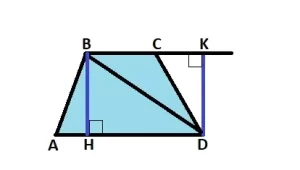
El trapecio dado: ABCD, AD y BC – longitudes de las bases, BH – altura.
Prueba: el área de este trapecio ABCD será igual a S = ½ (AD + BC) – BH.
Prueba: dibuja una diagonal BD. Divide el trapecio en dos triángulos ABD y BCD. Esto significa que el perímetro de un trapecio ABCD será igual a la suma de las áreas de estos triángulos.
En un triángulo ABD: AD es la base y BH es la altura. En un triángulo BCD: BC es la base.
Dibujemos la altura DK. El área S del triángulo ABD = 1/2 AD – BH; el área S del triángulo BCD = 1/2 BC – DK. Como BH = DK, entonces el área S del triángulo BCD = 1/2 BC – BH. Por tanto, el área S del trapecio ABCD = 1/2 AD – BH + 1/2 BC – BH = 1/2 (AD + BC) – BH. Lo que había que demostrar.
Cálculo de áreas en tiempos pasados
Incluso hace 4-5 mil años, los babilonios sabían cómo determinar el área de un trapecio en unidades cuadradas. Los antiguos egipcios de hace 4.000 años utilizaban casi los mismos trucos que nosotros: la suma de los lados paralelos se dividía por la mitad y se multiplicaba por la altura.
Determinar las áreas de las formas geométricas es uno de los problemas prácticos más antiguos. La gente no encontró inmediatamente el enfoque correcto para su solución. Una de las formas más sencillas y asequibles de calcular áreas fue descubierta por Euclides. Al calcular áreas, utilizó una técnica sencilla llamada método de partición.
El cálculo de áreas en el mundo moderno
Hoy en día existen muchas fórmulas para calcular las longitudes de los lados, los vértices, las bases paralelas y el área del trapecio. Vamos a cubrir las más básicas. Las fórmulas que se presentan a continuación son fáciles de usar, pero si te resulta difícil entenderlas y necesitas ayuda con los deberes, siempre puedes contactar con nuestro servicio. Autores experimentados te asesorarán en todas las tareas y mejorarás notablemente tu rendimiento académico.
Vídeos de Área de un trapecio rectángulo
Contenido