Funcion a trozos
Una función a trozos es una función f(x) que tiene diferentes definiciones en diferentes intervalos de x. La gráfica de una función a trozos tiene diferentes trozos correspondientes a cada una de sus definiciones. La función de valor absoluto es un muy buen ejemplo de función a trozos. Debemos leer esta función a trozos como
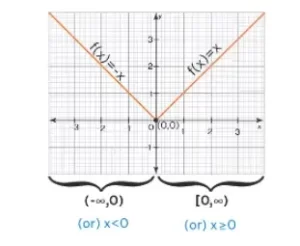
- f(x) es igual a x cuando x es mayor o igual a 0 y
- f(x) es igual a -x cuando x es menor que 0
- Entonces la gráfica de f(x) tiene dos trozos uno corresponde a x (cuando x está en el intervalo [0, ∞) ) y el otro trozo corresponde a -x (cuando x está en el intervalo (-∞, 0)). Su gráfica tiene el siguiente aspecto:

Gráfica de la función a trozos
Ya sabemos que la gráfica de una función a trozos tiene múltiples trozos donde cada trozo corresponde a su definición sobre un intervalo. Estos son los pasos para graficar una función a trozos.
- En primer lugar, entiende qué representa cada definición de la función. Por ejemplo, f(x) = ax + b representa una función lineal (que da una recta), f(x) = ax2 + bx + c representa una función cuadrática (que da una parábola), etc, de modo que tendremos una idea de qué forma tendría el trozo de la función.
- Escribe los intervalos que aparecen en la definición de la función junto con sus definiciones.
- Haz una tabla con dos columnas etiquetadas como x e y correspondientes a cada intervalo. Incluye sin falta los puntos extremos del intervalo. Si el punto final se excluye del intervalo, observa que obtenemos un punto abierto correspondiente a ese punto en la gráfica.
- En cada tabla, toma más números (números al azar) en la columna de x que estén en el intervalo correspondiente para obtener la forma perfecta de la gráfica. Si el trozo es una línea recta, entonces 2 valores para x son suficientes. Toma 3 o más números para x si el trozo NO es una línea recta.
- Sustituye cada valor de x de cada tabla en la definición correspondiente de la función para obtener los respectivos valores de y.
- Ahora, sólo tienes que trazar todos los puntos de la tabla (teniendo en cuenta los puntos abiertos) en una hoja de gráficos y unirlos mediante curvas.
Dominio y rango de la función a trozos
Para encontrar el dominio de una función a trozos, basta con mirar la definición de la función dada. Tomamos la unión de todos los intervalos con x y eso nos dará el dominio. En el ejemplo anterior, el dominio de f(x) es, {x | x < -2} U {x | -2 ≤ x ≤ 0} U {x | x > 0}. La unión de todos estos conjuntos es simplemente el conjunto de todos los números reales. Así que el dominio de f(x) (en el ejemplo anterior) es R.
Para encontrar el rango de una función a trozos, la forma más fácil es graficarla y mirar el eje y. Observa qué valores de y están cubiertos por la gráfica. En el ejemplo anterior, todos los valores de y menores que 2 (excluyendo 2 ya que hay un punto abierto en (0, 2)) están cubiertos por la gráfica. Así que su rango es {y | y < 2} (o) (-∞, 2).
Del mismo modo, podemos encontrar el dominio y el rango de cualquier función a trozos simplemente graficándola.
Vídeos de Funcion a trozos
Contenido