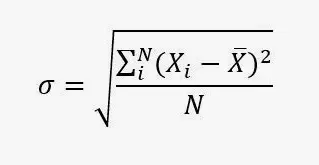Desviación típica fórmula
La desviación estándar es el grado de dispersión o la dispersión de los puntos de datos en relación con su media, en estadística descriptiva. Indica la dispersión de los valores en la muestra de datos y es la medida de la variación de los puntos de datos respecto a la media. La desviación estándar de una muestra, población estadística, variable aleatoria, conjunto de datos o distribución de probabilidad es la raíz cuadrada de su varianza.
Cuando tenemos un número n de observaciones y las observaciones son
x1,x2,…..xn, entonces la desviación media del valor de la media se determina como
∑ni=1(xi-¯x)2 . Sin embargo, la suma de los cuadrados de las desviaciones de la media no parece ser una medida adecuada de la dispersión. Si la media de las diferencias al cuadrado respecto a la media es pequeña, indica que las observaciones
xi están cerca de la media
¯x. Se trata de un grado de dispersión menor. Si esta suma es grande, indica que hay un mayor grado de dispersión de las observaciones con respecto a la media
¯x. Por lo tanto, concluimos que
∑ni=1(xi-¯x)2
es un indicador razonable del grado de dispersión o dispersión.
Tomamos
1 n ∑ n i = 1 ( x i – ¯ x ) 2 como medida propia de la dispersión y se denomina varianza(σ2). La raíz cuadrada de la varianza es la desviación estándar.
Pasos para calcular la desviación estándar
Encuentre la media, que es la media aritmética de las observaciones.
Hallar las diferencias al cuadrado con respecto a la media. (El valor de los datos – la media)2
Hallar la media de las diferencias al cuadrado. (Varianza = La suma de las diferencias al cuadrado ÷ el número de observaciones)
Encuentra la raíz cuadrada de la varianza. (Desviación estándar = √Varianza)
Fórmula de la desviación estándar
La dispersión de los datos estadísticos se mide por la desviación estándar. El grado de dispersión se calcula mediante el método de estimación de la desviación de los puntos de datos. Se puede leer sobre la dispersión en las estadísticas resumidas. Como se ha dicho, la varianza del conjunto de datos es la distancia cuadrada media entre el valor medio y cada valor de los datos. Y la desviación estándar define la dispersión de los valores de los datos alrededor de la media. Aquí hay dos fórmulas de desviación estándar que se utilizan para encontrar la desviación estándar de los datos de la muestra y la desviación estándar de la población dada.
Desviación estándar de datos no agrupados
Los cálculos de la desviación estándar difieren para los distintos datos. La distribución mide la desviación de los datos respecto a su media o posición media. Hay dos métodos para encontrar la desviación estándar.
método de la media real
método de la media supuesta
Desviación estándar de las variables aleatorias
La medida de dispersión de la distribución de probabilidad de una variable aleatoria determina el grado en que los valores difieren del valor esperado. Es una función que asigna un valor numérico a cada resultado en un espacio muestral. Se denota por X, Y o Z, ya que es una función. Si X es una variable aleatoria, la desviación estándar se determina tomando la raíz cuadrada de la suma del producto de la diferencia al cuadrado entre la variable aleatoria, x, y el valor esperado () y el valor asociado a la probabilidad de la variable aleatoria.
La desviación estándar de la distribución de probabilidad de X, =√ ( x – μ ) 2 P ( X = x )
Desviación estándar de la distribución de la probabilidad
La probabilidad experimental se compone de muchos ensayos. Cuando la diferencia entre la probabilidad teórica de un suceso y su frecuencia relativa se acercan, tendemos a conocer el resultado medio. Esta media se conoce como el valor esperado del experimento denotado por .
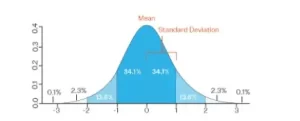
- En una distribución normal, la media es cero y la desviación estándar es 1.
- En un experimento binomial, el número de aciertos es una variable aleatoria. Si una variable aleatoria tiene una distribución binomial, su desviación típica viene dada por: = √npq, donde media: = np, n = número de ensayos, p = probabilidad de éxito y 1-p =q es la probabilidad de fracaso.
- En una distribución de Poisson, la desviación estándar viene dada por = √λt, donde λ es el número medio de éxitos en un intervalo de tiempo t.
Vídeos de Desviación típica fórmula
Contenido