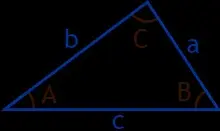
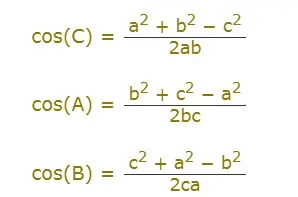Área del triángulo con 3 lados
Para encontrar el área de un triángulo de 3 lados, utilizamos la fórmula de Herón. El área de un triángulo se puede calcular con la ayuda de varias fórmulas. La fórmula básica que se utiliza para hallar el área de un triángulo es ½ × Base × Altura donde «Base» es el lado del triángulo en el que se forma la altitud, y «Altura» es la longitud de la altitud trazada a la «Base» desde su vértice opuesto. Sin embargo, si no se conoce la altitud de un triángulo, y necesitamos encontrar el área de un triángulo con 3 lados diferentes, se utiliza la fórmula de Herón. Esta fórmula fue derivada por un matemático griego conocido como Herón de Alejandría.
Fórmula del área de un triángulo de 3 lados
Para encontrar el área de un triángulo con 3 lados, se utiliza la fórmula de Herón que dice que si a, b y c son los tres lados de un triángulo, entonces su área es,
Área = √[s(s-a)(s-b)(s-c)]
Aquí, «s» es el semiperímetro del triángulo, es decir, s = (a + b + c)/2.
Como calcular los ángulos de un triángulo sabiendo sus lados
«SSS» es cuando conocemos tres lados del triángulo y queremos encontrar los ángulos que faltan.
Para resolver un triángulo SSS
- usar la Ley de los Cosenos primero para calcular uno de los ángulos
- a continuación, utilizar la ley de los cosenos de nuevo para encontrar otro ángulo
- y, finalmente, utilizar los ángulos de un triángulo que suman 180° para encontrar el último ángulo.
Vídeos de Como calcular los ángulos de un triángulo sabiendo sus lados
Contenido